


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-2-2016
Date: 2-10-2021
Date: 15-9-2021
|
A game played with two heaps of counters in which a player may take any number from either heap or the same number from both. The player taking the last counter wins. The 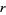 th safe combination is
th safe combination is 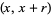 , where
, where 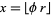 , with
, with 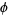 the golden ratio and
the golden ratio and 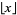 the floor function. It is also true that
the floor function. It is also true that 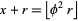 . The first few safe combinations are (1, 2), (3, 5), (4, 7), (6, 10), ... (OEIS A000201 and A001950), which are the pairs of elements from the complementary Beatty sequences for
. The first few safe combinations are (1, 2), (3, 5), (4, 7), (6, 10), ... (OEIS A000201 and A001950), which are the pairs of elements from the complementary Beatty sequences for 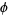 and
and 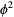 (Wells 1986, p. 40).
(Wells 1986, p. 40).
REFERENCES:
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 39-40, 1987.
Coxeter, H. S. M. "The Golden Section, Phyllotaxis, and Wythoff's Game." Scripta Math. 19, 135-143, 1953.
O'Beirne, T. H. Puzzles and Paradoxes. Oxford, England: Oxford University Press, pp. 109 and 134-138, 1965.
Sloane, N. J. A. Sequences A000201/M2322 and A001950/M1332 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 40, 1986.
Wythoff, W. A. "A Modification of the Game of Nim." Nieuw Arch. Wisk. 8, 199-202, 1907/1909.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|