Strange Attractor

An attracting set that has zero measure in the embedding phase space and has fractal dimension. Trajectories within a strange attractor appear to skip around randomly.

A selection of strange attractors for a general quadratic map

			(1)
			(2)

are illustrated above, where the letters 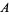 to 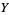 stand for coefficients of the quadratic from  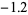to 1.2 in steps of 0.1 (Sprott 1993c). These represent a small selection of the approximately 1.6% of all possible  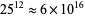such maps that are chaotic (Sprott 1993bc).

REFERENCES:

Benmizrachi, A.; Procaccia, I.; and Grassberger, P. "Characterization of Experimental (Noisy) Strange Attractors." Phys. Rev. A 29, 975-977, 1984.

Dewdney, A. K. "Probing the Strange Attractors of Chaos." Sci. Amer. 235, 90-93, 1976.

Farmer, J. D.; Ott, E.; and Yorke, J. A. "The Dimension of Chaotic Attractors." Physica 7D, 153, 1983.

Gleick, J. "Strange Attractors." Chaos: Making a New Science. New York: Penguin Books, pp. 119-153, 1988.

Grassberger, P. "On the Hausdorff Dimension of Fractal Attractors." J. Stat. Phys. 26, 173-179, 1981.

Grassberger, P. and Procaccia, I. "Measuring the Strangeness of Strange Attractors." Physica D 9, 189-208, 1983a.

Grassberger, P. and Procaccia, I. "Characterization of Strange Attractors." Phys. Rev. Let. 50, 346-349, 1983b.

Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 137-138, 1991.

Peitgen, H.-O. and Richter, D. H. The Beauty of Fractals: Images of Complex Dynamical Systems. New York: Springer-Verlag, 1986.

Pickover, C. "A Note on Rendering 3-D Strange-Attractors." Comput. & Graphics 12, 263, 1988.

Sprott, J. C. Strange Attractors: Creating Patterns in Chaos. New York: Henry Holt, 1993a.

Sprott, J. C. "How Common Is Chaos?" Phys. Lett. A 173, 21, 1993b.

Sprott, J. C. "Automatic Generation of Strange Attractors." Comput. & Graphics 17, 325-332, 1993c. Reprinted in Chaos and Fractals, A Computer Graphical Journey: Ten Year Compilation of Advanced Research (Ed. C. A. Pickover). Amsterdam, Netherlands: Elsevier, pp. 53-60, 1998.

Viana, M. "What's New on Lorenz Strange Attractors." Math. Intell. 22, 6-19.