


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-10-2021
Date: 25-9-2021
Date: 28-9-2021
|
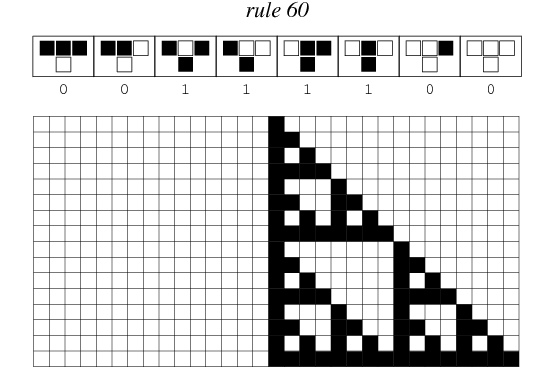
Rule 60 is one of the elementary cellular automaton rules introduced by Stephen Wolfram in 1983 (Wolfram 1983, 2002). It specifies the next color in a cell, depending on its color and its immediate neighbors. Its rule outcomes are encoded in the binary representation 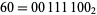 . This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (OEIS A075438; Wolfram 2002, p. 55).
. This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (OEIS A075438; Wolfram 2002, p. 55).
Starting with a single black cell, successive generations are given by interpreting the numbers 1, 3, 5, 15, 17, 51, 85, 255, 257, 771, 1285, ... (OEIS A001317) in binary (where left 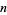 cells in step
cells in step 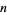 of the triangle are always 0), namely 1, 11, 101, 1111, 10001; ... (OEIS A047999).
of the triangle are always 0), namely 1, 11, 101, 1111, 10001; ... (OEIS A047999).
The mirror image is rule 102, the complement is rule 195, and the mirrored complement is rule 153.

Rule 60 is one of the eight additive elementary cellular automata (Wolfram 2002, p. 952).
REFERENCES:
Sloane, N. J. A. Sequences A001317/M2495, A047999, and A075438 in "The On-Line Encyclopedia of Integer Sequences."
Wolfram, S. "Statistical Mechanics of Cellular Automata." Rev. Mod. Phys. 55, 601-644, 1983.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 90 and 952-953, 2002.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
أولياء أمور الطلبة يشيدون بمبادرة العتبة العباسية بتكريم الأوائل في المراحل المنتهية
|
|
|