Tetrix

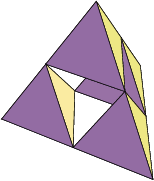
The tetrix is the three-dimensional analog of the Sierpiński sieve illustrated above, also called the Sierpiński sponge or Sierpiński tetrahedron.

The th iteration of the tetrix is implemented in the Wolfram Language as SierpinskiMesh[n, 3].

Let  be the number of tetrahedra,  the length of a side, and  the fractional volume of tetrahedra after the th iteration. Then

			(1)
			(2)
			(3)

The capacity dimension is therefore

			(4)
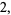			(5)

so the tetrix has an integer capacity dimension (which is one less than the dimension of the three-dimensional tetrahedra from which it is built), despite the fact that it is a fractal.

The following illustrations demonstrate how the dimension of the tetrix can be the same as that of the plane by showing three stages of the rotation of a tetrix, viewed along one of its edges. In the last frame, the tetrix "looks" like the two-dimensional plane.

REFERENCES:

Allanson, B. "The Fractal Tetrahedron" java applet. http://members.ozemail.com.au/~llan/Fractet.html.

Borwein, J. and Bailey, D. "Pascal's Triangle." §2.1 in Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 46-47, 2003.

Dickau, R. M. "Sierpinski Tetrahedron." http://mathforum.org/advanced/robertd/tetrahedron.html.

Eppstein, D. "Sierpinski Tetrahedra and Other Fractal Sponges." http://www.ics.uci.edu/~eppstein/junkyard/sierpinski.html.

Kabai, S. Mathematical Graphics I: Lessons in Computer Graphics Using Mathematica. Püspökladány, Hungary: Uniconstant, pp. 159-160, 2002.

Kosmulski, M. "Modulus Origami--Fractals, IFS." http://hektor.umcs.lublin.pl/~mikosmul/origami/fractals.html.

Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, pp. 142-143, 1983.