Arcwise-Connected

Many authors (e.g., Mendelson 1963; Pervin 1964) use the term arcwise-connected as a synonym for pathwise-connected. Other authors (e.g., Armstrong 1983; Cullen 1968; and Kowalsky 1964) use the term to refer to a stronger type of connectedness, namely that an arc connecting two points 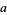 and 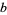 of a topological space  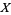is not simply (like a path) a continuous function  such that 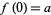 and 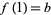, but must also have a continuous inverse function, i.e., that it is a homeomorphism between  and the image of .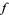

The difference between the two notions can be clarified by a simple example. The set 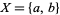 with the trivial topology is pathwise-connected, but not arcwise-connected since the function  defined by 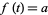 for all 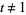, and 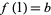, is a path from  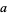to 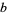, but there exists no homeomorphism from  to 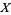, since even injectivity is impossible.

Arcwise- and pathwise-connected are equivalent in Euclidean spaces and in all topological spaces having a sufficiently rich structure. In particular theorem states that every locally compact, connected, locally connected metrizable topological space is arcwise-connected (Cullen 1968, p. 327).

REFERENCES:

Armstrong, M. A. Basic Topology, rev. ed. New York: Springer-Verlag, p. 112, 1997.

Cullen, H. F. Introduction to General Topology. Boston, MA: Heath, pp. 325-330, 1968.

Kowalsky, H. J. Topological Spaces. New York: Academic Press, p. 183, 1964.

Mendelson, B. Introduction to Topology. London, England: Blackie & Son, 1963.

Pervin, W. J. "Arcwise Connectivity." §4.5 in Foundations of General Topology. New York: Academic Press, pp. 67-68, 1964.