


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-6-2021
Date: 26-9-2016
Date: 15-7-2021
|
A quaternion Kähler manifold is a Riemannian manifold of dimension 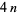 ,
, 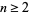 , whose holonomy is, up to conjugacy, a subgroup of
, whose holonomy is, up to conjugacy, a subgroup of
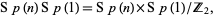 |
but is not a subgroup of 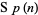 . These manifolds are sometimes called quaternionic Kähler and are sometimes written hyphenated as quaternion-Kähler, quaternionic-Kähler, etc.
. These manifolds are sometimes called quaternionic Kähler and are sometimes written hyphenated as quaternion-Kähler, quaternionic-Kähler, etc.
Despite their name, quaternion-Kähler manifolds need not be Kähler due to the fact that all Kähler manifolds have holonomy groups which are subgroups of 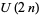 , whereas
, whereas 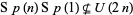 . Depending on the literature, such manifolds are sometimes assumed to be connected and/or orientable. In the above definition, the case for
. Depending on the literature, such manifolds are sometimes assumed to be connected and/or orientable. In the above definition, the case for 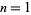 is usually excluded due to the fact that
is usually excluded due to the fact that 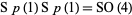 which, under Berger's classification of holonomy, implies merely that the manifold is Riemannian. The above classification can be extended to the case where
which, under Berger's classification of holonomy, implies merely that the manifold is Riemannian. The above classification can be extended to the case where 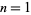 by requiring that the manifold be both an Einstein manifold and self-dual.
by requiring that the manifold be both an Einstein manifold and self-dual.
Some authors exclude this last criterion, thereby classifying manifolds as quaternion-Kähler provided that they are Riemannian and have a holonomy group which is a subgroup of 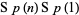 . Under this less-restrictive definition, Hyper-Kähler manifolds-manifolds with holonomy group a subgroup of
. Under this less-restrictive definition, Hyper-Kähler manifolds-manifolds with holonomy group a subgroup of 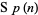 -would be considered quaternion-Kähler, though it is not uncommon for literature to distinguish between manifolds which are quaternion-Kähler and hypkerkähler. In place of the last criterion, some authors instead impose the condition that the manifold have nonzero scalar curvature, whereby manifolds which are hypkerkähler (and hence are Ricci-flat) are again precluded.
-would be considered quaternion-Kähler, though it is not uncommon for literature to distinguish between manifolds which are quaternion-Kähler and hypkerkähler. In place of the last criterion, some authors instead impose the condition that the manifold have nonzero scalar curvature, whereby manifolds which are hypkerkähler (and hence are Ricci-flat) are again precluded.
Berger showed that for 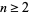 , quaternionic-Kähler manifolds are necessarily Einstein manifolds.
, quaternionic-Kähler manifolds are necessarily Einstein manifolds.
Because the definition of quaternion-Kähler manifolds excludes the possibility of having zero scalar curvature, it is natural to investigate the cases of quaternion-Kähler manifolds with positive and negative scalar curvatures (referred to as positive quaternion-Kähler and negative quaternion-Kähler manifolds, respectively) separately. The work of LeBrun shows a number of significant differences in these two cases, and while many advances have been made towards the understanding of positive quaternion-Kähler manifolds, little seems to be known regarding their negative scalar curvature counterparts.
There are no known examples of compact quaternion Kähler manifolds which are neither locally symmetric nor hyper-Kähler. Moreover, it has been conjectured by LeBrun among others that all positive quaternion-Kähler manifolds are symmetric with proved confirmation for dimensions 4 and 8. Quaternion-Kähler manifolds which are locally symmetric are known as Wolf spaces.
REFERENCES:
Amann, M. "Positive Quaternion Kähler Manifolds." Doctoral Thesis, 2009.
Amann, M. "Partial Classification Results for Positive Quaternion Kähler Manifolds." 24 Nov 2009. https://arxiv-web3.library.cornell.edu/pdf/0911.4587v1.pdf.
Berger, M. "Sur les groupes d'holonomie homogènes de variétès à conexion affine et des variétès riemanniennes." Bull. Soc. Math. France 283, 279-330, 1955.
LeBrun, C. "On Complete Quaternionic-Kähler Manifolds." Duke Math. J. 63, 723-743, 1991.



|
|
|
|
للحفاظ على صحة العين.. تناول هذا النوع من المكسرات
|
|
|
|
|
|
|
COP29.. رئيس الإمارات يؤكد أهمية تسريع العمل المناخي
|
|
|
|
|
|
|
الامين العام للعتبة الحسينية يؤكد على هيئة التعليم التقني بتحقيق التنمية المستدامة في البلاد
|
|
|