Alexander Invariant

The Alexander invariant 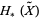 of a knot  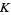is the homology of the infinite cyclic cover of the complement of 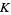, considered as a module over 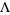, the ring of integral laurent polynomials. The Alexander invariant for a classical tame knot is finitely presentable, and only  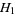is significant.

For any knot 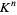 in 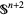 whose complement has the homotopy type of a finite CW-complex, the Alexander invariant is finitely generated and therefore finitely presentable. Because the Alexander invariant of a tame knot in  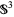has a square presentation matrix, its Alexander ideal is principal and it has an Alexander polynomial denoted .

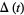REFERENCES:

Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 206-207, 1976.