المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Difference of Successes |
 1305
 04:28 مساءً
date: 4-4-2021 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : www.almerja.com 
Page and Part : ...|
Read More
Date: 25-3-2021
1220
Date: 22-3-2021
1734
Date: 14-2-2016
1513
|
If 
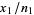and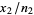 
are the observed proportions from standard normally distributed samples with proportion of success 
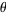, then the probability that
 |
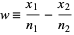(1) |
will be as great as observed is
 |
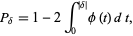(2) |
where
 |
 |
 |
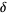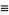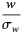(3) |
 |
 |
 |
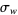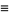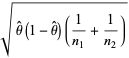(4) |
 |
 |
 |
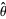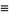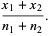(5) |
Here,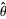 
is the unbiased estimator. The skewness and kurtosis excess of this distribution are
 |
 |
 |
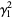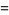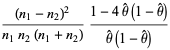(6) |
 |
 |
 |
|
|
|
|
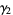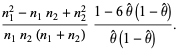تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
