المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Wiener Sausage |
 1179
 05:26 مساءً
date: 25-3-2021 |
Author : Bolthausen, E. 
Book or Source : "On the Volume of the Wiener Sausage." Ann. Prob. 18 
Page and Part : ...|
Read More
Date: 27-3-2021
1677
Date: 16-4-2021
2019
Date: 2-5-2021
2574
|
The Wiener sausage of radius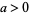 
is the random process defined by
 |
where here,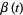 
is the standard Brownian motion in 
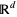for 
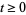and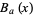 
denotes the open ball of radius 
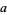centered at 
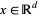. Named after Norbert Wiener, the term is also intended to describe 
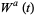visually: Indeed, for a given Brownian motion 
, 
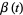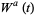is essentially a sausage-like tube of radius 
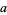having 
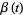as its central line.
REFERENCES:
Bolthausen, E. "On the Volume of the Wiener Sausage." Ann. Prob. 18, 1576-1582, 1990.
van den Berg, M.; Bolthausen, E.; and den Hollander, F. "On the Volume of the Intersection of Two Wiener Sausages." Ann. Math. 159, 741-783, 2004.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|
