المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Strong Frobenius Pseudoprime |
 602
 03:32 مساءً
date: 25-1-2021 |
Author : Grantham, J 
Book or Source : "Frobenius Pseudoprimes." 1996. https://www.clark.net/pub/grantham/pseudo/pseudo1.ps. 
Page and Part : ...|
Read More
Date: 26-8-2020
783
Date: 9-8-2020
560
Date: 11-11-2020
637
|
A pseudoprime which obeys an additional restriction beyond that required for a Frobenius pseudoprime. A number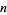 
with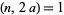 
is a strong Frobenius pseudoprime with respect to 
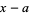iff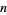 
is a strong pseudoprime with respect to 
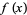. Every strong Frobenius pseudoprime with respect to 
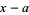is an Euler pseudoprime to the base 
.
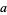Every strong Frobenius pseudoprime with respect to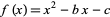 
such that 
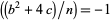is a strong Lucas pseudoprime with parameters 
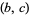. Every strong Frobenius pseudoprime 
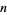with respect to 
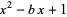is an extra strong Lucas pseudoprime to the base 
.
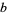REFERENCES:
Grantham, J. "Frobenius Pseudoprimes." 1996. https://www.clark.net/pub/grantham/pseudo/pseudo1.ps.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
