


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-6-2020
Date: 8-3-2020
Date: 16-7-2020
|

A square number, also called a perfect square, is a figurate number of the form 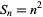 , where
, where 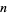 is an integer. The square numbers for
is an integer. The square numbers for 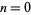 , 1, ... are 0, 1, 4, 9, 16, 25, 36, 49, ... (OEIS A000290).
, 1, ... are 0, 1, 4, 9, 16, 25, 36, 49, ... (OEIS A000290).

A plot of the first few square numbers represented as a sequence of binary bits is shown above. The top portion shows 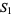 to
to 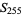 , and the bottom shows the next 510 values.
, and the bottom shows the next 510 values.
The generating function giving the square numbers is
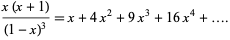 |
(1) |
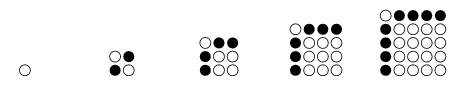
The 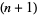 st square number
st square number 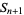 is given in terms of the
is given in terms of the 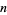 th square number
th square number 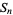 by
by
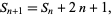 |
(2) |
since
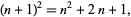 |
(3) |
which is equivalent to adding a gnomon to the previous square, as illustrated above.

The 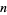 th square number is equal to the sum of the
th square number is equal to the sum of the 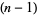 st and
st and 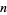 th triangular numbers,
th triangular numbers,
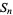 |
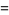 |
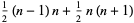 |
(4) |
 |
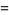 |
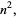 |
(5) |
as can seen in the above diagram, in which the 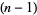 st triangular number is represented by the white triangles, the
st triangular number is represented by the white triangles, the 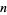 th triangular number is represented by the black triangles, and the total number of triangles is the square number
th triangular number is represented by the black triangles, and the total number of triangles is the square number 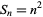 (R. Sobel, pers. comm.).
(R. Sobel, pers. comm.).
Square numbers can also be generated by taking the product of two consecutive even or odd numbers and adding 1. The result obtained by carrying out this operation is then the square of the average of the initial two numbers,
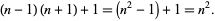 |
(6) |
As a part of the study of Waring's problem, it is known that every positive integer is a sum of no more than 4 positive squares (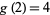 ; Lagrange's four-square theorem), that every "sufficiently large" integer is a sum of no more than 4 positive squares (
; Lagrange's four-square theorem), that every "sufficiently large" integer is a sum of no more than 4 positive squares (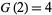 ), and that every integer is a sum of at most 3 signed squares (
), and that every integer is a sum of at most 3 signed squares (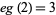 ). Actually, the basis set for representing positive integers with positive squares is
). Actually, the basis set for representing positive integers with positive squares is 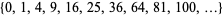 , so 49 need never be used. Furthermore, since an infinite number of
, so 49 need never be used. Furthermore, since an infinite number of  require four squares to represent them, the least integer
require four squares to represent them, the least integer  such that every positive integer beyond a certain point requires
such that every positive integer beyond a certain point requires  squares is given by
squares is given by 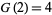 .
.
The number of representation of a number 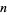 by
by 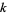 squares, distinguishing signs and order, is denoted
squares, distinguishing signs and order, is denoted 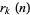 and called the sum of squares function. The minimum number of squares needed to represent the numbers 1, 2, 3, ... are 1, 2, 3, 1, 2, 3, 4, 2, 1, 2, ... (OEIS A002828), and the number of distinct ways to represent the numbers 1, 2, 3, ... in terms of squares are 1, 1, 1, 2, 2, 2, 2, 3, 4, 4, ... (OEIS A001156). A brute-force algorithm for enumerating the square partitions of
and called the sum of squares function. The minimum number of squares needed to represent the numbers 1, 2, 3, ... are 1, 2, 3, 1, 2, 3, 4, 2, 1, 2, ... (OEIS A002828), and the number of distinct ways to represent the numbers 1, 2, 3, ... in terms of squares are 1, 1, 1, 2, 2, 2, 2, 3, 4, 4, ... (OEIS A001156). A brute-force algorithm for enumerating the square partitions of 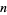 is repeated application of the greedy algorithm. However, this approach rapidly becomes impractical since the number of representations grows extremely rapidly with
is repeated application of the greedy algorithm. However, this approach rapidly becomes impractical since the number of representations grows extremely rapidly with 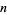 , as shown in the following table.
, as shown in the following table.
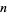 |
square partitions |
| 10 | 4 |
| 50 | 104 |
| 100 | 1116 |
| 150 | 6521 |
| 200 | 27482 |
The 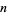 th nonsquare number
th nonsquare number 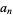 is given by
is given by
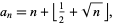 |
(7) |
where 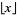 is the floor function, and the first few are 2, 3, 5, 6, 7, 8, 10, 11, ... (OEIS A000037).
is the floor function, and the first few are 2, 3, 5, 6, 7, 8, 10, 11, ... (OEIS A000037).
The only numbers that are simultaneously square and pyramidal (the cannonball problem) are 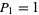 and
and 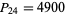 , corresponding to
, corresponding to 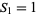 and
and 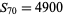 (Ball and Coxeter 1987, p. 59; Ogilvy 1988; Dickson 2005, p. 25), as conjectured by Lucas (1875, 1876) and proved by Watson (1918). The cannonball problem is equivalent to solving the Diophantine equation
(Ball and Coxeter 1987, p. 59; Ogilvy 1988; Dickson 2005, p. 25), as conjectured by Lucas (1875, 1876) and proved by Watson (1918). The cannonball problem is equivalent to solving the Diophantine equation
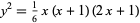 |
(8) |
(Guy 1994, p. 147).
The only numbers that are square and tetrahedral are 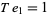 ,
, 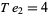 , and
, and 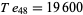 (giving
(giving 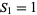 ,
, 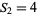 , and
, and 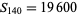 ), as proved by Meyl (1878; cited in Dickson 2005, p. 25; Guy 1994, p. 147). In general, proving that only certain numbers are simultaneously figurate in two different ways is far from elementary.
), as proved by Meyl (1878; cited in Dickson 2005, p. 25; Guy 1994, p. 147). In general, proving that only certain numbers are simultaneously figurate in two different ways is far from elementary.
To find the possible last digits for a square number, write 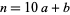 for the number written in decimal notation as
for the number written in decimal notation as 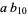 (
(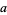 ,
, 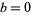 , 1, ..., 9). Then
, 1, ..., 9). Then
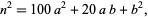 |
(9) |
so the last digit of 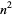 is the same as the last digit of
is the same as the last digit of 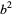 . The following table gives the last digit of
. The following table gives the last digit of 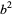 for
for 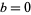 , 1, ..., 9 (where numbers with more that one digit have only their last digit indicated, i.e., 16 becomes _6). As can be seen, the last digit can be only 0, 1, 4, 5, 6, or 9.
, 1, ..., 9 (where numbers with more that one digit have only their last digit indicated, i.e., 16 becomes _6). As can be seen, the last digit can be only 0, 1, 4, 5, 6, or 9.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 4 | 9 | _6 | _5 | _6 | _9 | _4 | _1 |
We can similarly examine the allowable last two digits by writing 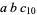 as
as
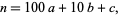 |
(10) |
so
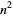 |
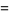 |
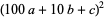 |
(11) |
 |
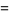 |
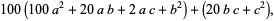 |
(12) |
so the last two digits must have the last two digits of 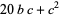 . Furthermore, the last two digits can be obtained by considering only
. Furthermore, the last two digits can be obtained by considering only 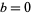 , 1, 2, 3, and 4, since
, 1, 2, 3, and 4, since
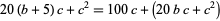 |
(13) |
has the same last two digits as 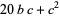 (with the one additional possibility that
(with the one additional possibility that  in which case the last two digits are 00). The following table (with the addition of 00) therefore exhausts all possible last two digits.
in which case the last two digits are 00). The following table (with the addition of 00) therefore exhausts all possible last two digits.
 |
|||||||||
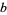 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 01 | 04 | 09 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | _21 | _44 | _69 | _96 | _25 | _56 | _89 | _24 | _61 |
| 2 | _41 | _84 | _29 | _76 | _25 | _76 | _29 | _84 | _41 |
| 3 | _61 | _24 | _89 | _56 | _25 | _96 | _69 | _44 | _21 |
| 4 | _81 | _64 | _49 | _36 | _25 | _16 | _09 | _04 | _01 |
The only 22 possibilities are therefore 00, 01, 04, 09, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89, and 96, which can be summarized succinctly as 00, 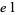 ,
, 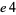 , 25,
, 25, 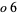 , and
, and 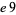 , where
, where 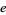 stands for an even number and
stands for an even number and 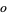 for an odd number. Additionally, a necessary (but not sufficient) condition for a number to be square is that its digital root be 1, 4, 7, or 9. The digital roots of the first few squares are 1, 4, 9, 7, 7, 9, 4, 1, 9, 1, 4, 9, 7, ... (OEIS A056992), while the list of number having digital roots 1, 4, 7, or 9 is 1, 4, 7, 9, 10, 13, 16, 18, 19, 22, 25, ... (OEIS A056991).
for an odd number. Additionally, a necessary (but not sufficient) condition for a number to be square is that its digital root be 1, 4, 7, or 9. The digital roots of the first few squares are 1, 4, 9, 7, 7, 9, 4, 1, 9, 1, 4, 9, 7, ... (OEIS A056992), while the list of number having digital roots 1, 4, 7, or 9 is 1, 4, 7, 9, 10, 13, 16, 18, 19, 22, 25, ... (OEIS A056991).
This property of square numbers was referred to in a "puzzler" feature of a March 2008 broadcast of the NPR radio show "Car Talk." In this Puzzler, a son tells his father that his computer and math teacher assigned the class a problem to determine if a number is a perfect square. Each student is assigned a particular number, and the students are supposed to write a software program to determine the answer. The son's assigned number was 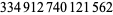 . While the father thinks this is a hard problem, a bystander listening to the conversation states that the teacher gave the son an easy number and the bystander can give the answer immediately. The question is what does this third person know? The answer is that the number ends in the digit "2," which is not one of the possible last digits for a square number.
. While the father thinks this is a hard problem, a bystander listening to the conversation states that the teacher gave the son an easy number and the bystander can give the answer immediately. The question is what does this third person know? The answer is that the number ends in the digit "2," which is not one of the possible last digits for a square number.
The following table gives the possible residues mod 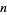 for square numbers for
for square numbers for 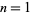 to 20. The quantity
to 20. The quantity 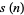 gives the number of distinct residues for a given
gives the number of distinct residues for a given 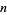 .
.
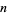 |
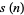 |
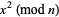 |
| 2 | 2 | 0, 1 |
| 3 | 2 | 0, 1 |
| 4 | 2 | 0, 1 |
| 5 | 3 | 0, 1, 4 |
| 6 | 4 | 0, 1, 3, 4 |
| 7 | 4 | 0, 1, 2, 4 |
| 8 | 3 | 0, 1, 4 |
| 9 | 4 | 0, 1, 4, 7 |
| 10 | 6 | 0, 1, 4, 5, 6, 9 |
| 11 | 6 | 0, 1, 3, 4, 5, 9 |
| 12 | 4 | 0, 1, 4, 9 |
| 13 | 7 | 0, 1, 3, 4, 9, 10, 12 |
| 14 | 8 | 0, 1, 2, 4, 7, 8, 9, 11 |
| 15 | 6 | 0, 1, 4, 6, 9, 10 |
| 16 | 4 | 0, 1, 4, 9 |
| 17 | 9 | 0, 1, 2, 4, 8, 9, 13, 15, 16 |
| 18 | 8 | 0, 1, 4, 7, 9, 10, 13, 16 |
| 19 | 10 | 0, 1, 4, 5, 6, 7, 9, 11, 16, 17 |
| 20 | 6 | 0, 1, 4, 5, 9, 16 |
In general, the odd squares are congruent to 1 (mod 8) (Conway and Guy 1996). Stangl (1996) gives an explicit formula by which the number of squares 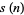 in
in 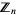 (i.e., mod
(i.e., mod 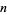 ) can be calculated. Let
) can be calculated. Let 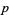 be an odd prime. Then
be an odd prime. Then 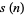 is the multiplicative function given by
is the multiplicative function given by
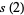 |
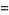 |
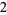 |
(14) |
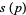 |
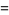 |
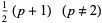 |
(15) |
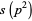 |
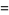 |
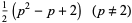 |
(16) |
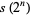 |
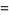 |
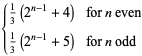 |
(17) |
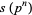 |
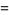 |
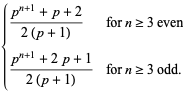 |
(18) |
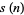 is related to the number
is related to the number 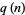 of quadratic residues in
of quadratic residues in 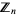 by
by
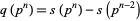 |
(19) |
for 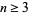 (Stangl 1996).
(Stangl 1996).
For a perfect square 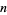 ,
, 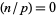 or 1 for all odd primes
or 1 for all odd primes 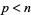 where
where 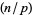 is the Legendre symbol. A number
is the Legendre symbol. A number 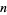 that is not a perfect square but that satisfies this relationship is called a pseudosquare.
that is not a perfect square but that satisfies this relationship is called a pseudosquare.
In a Ramanujan conference talk, W. Gosper conjectured that every sum of four distinct odd squares is the sum of four distinct even squares. This conjecture was proved by M. Hirschhorn using the identity
![(4a+1)^2+(4b+1)^2+(4c+1)^2+(4d+1)^2
=4[(a+b+c+d+1)^2+(a-b-c+d)^2+(a-b+c-d)^2+(a+b-c-d)^2],](https://mathworld.wolfram.com/images/equations/SquareNumber/NumberedEquation11.gif) |
(20) |
where 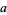 ,
, 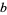 ,
, 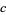 , and
, and 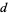 are positive or negative integers. Hirschhorn also showed that every sum of four distinct oddly even squares is the sum of four distinct odd squares.
are positive or negative integers. Hirschhorn also showed that every sum of four distinct oddly even squares is the sum of four distinct odd squares.
A prime number 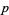 can be written as the sum of two squares iff
can be written as the sum of two squares iff 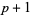 is not divisible by 4 the (Fermat's 4n+1 theorem). An arbitrary positive number
is not divisible by 4 the (Fermat's 4n+1 theorem). An arbitrary positive number 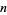 is expressible as the sum of two squares iff, given its prime factorization
is expressible as the sum of two squares iff, given its prime factorization
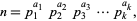 |
(21) |
none of 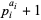 is divisible by 4 (Conway and Guy 1996, p. 147). This is equivalent the requirement that all the odd factors of the squarefree part
is divisible by 4 (Conway and Guy 1996, p. 147). This is equivalent the requirement that all the odd factors of the squarefree part 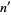 of
of 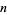 are equal to 1 (mod 4) (Hardy and Wright 1979, Finch). The first few numbers that can be expressed as the sum of two squares are 1, 2, 4, 5, 8, 9, 10, 13, 16, 17, 18, 20, 25, 26, ... (OEIS A001481). Letting
are equal to 1 (mod 4) (Hardy and Wright 1979, Finch). The first few numbers that can be expressed as the sum of two squares are 1, 2, 4, 5, 8, 9, 10, 13, 16, 17, 18, 20, 25, 26, ... (OEIS A001481). Letting 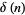 be the fraction of numbers
be the fraction of numbers 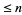 that are expressible as the sum of two squares,
that are expressible as the sum of two squares,
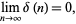 |
(22) |
and
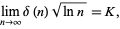 |
(23) |
where 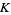 is the Landau-Ramanujan constant.
is the Landau-Ramanujan constant.
Numbers expressible as the sum of three squares are those not of the form 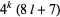 for
for 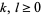 (Nagell 1951, p. 194; Wells 1986, pp. 48 and 56; Hardy 1999, p. 12).
(Nagell 1951, p. 194; Wells 1986, pp. 48 and 56; Hardy 1999, p. 12).
The following table gives the first few numbers which require 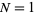 , 2, 3, and 4 squares to represent them as a sum (Wells 1986, p. 70).
, 2, 3, and 4 squares to represent them as a sum (Wells 1986, p. 70).
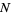 |
Sloane | numbers |
| 1 | A000290 | 1, 4, 9, 16, 25, 36, 49, 64, 81, ... |
| 2 | A000415 | 2, 5, 8, 10, 13, 17, 18, 20, 26, 29, ... |
| 3 | A000419 | 3, 6, 11, 12, 14, 19, 21, 22, 24, 27, ... |
| 4 | A004215 | 7, 15, 23, 28, 31, 39, 47, 55, 60, 63, ... |
Fermat's 4n+1 theorem guarantees that every prime of the form 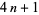 is a sum of two square numbers in only one way.
is a sum of two square numbers in only one way.
There are only 31 numbers that cannot be expressed as the sum of distinct squares: 2, 3, 6, 7, 8, 11, 12, 15, 18, 19, 22, 23, 24, 27, 28, 31, 32, 33, 43, 44, 47, 48, 60, 67, 72, 76, 92, 96, 108, 112, 128 (OEIS A001422; Guy 1994; Savin 2000). The following numbers cannot be represented using fewer than five distinct squares: 55, 88, 103, 132, 172, 176, 192, 240, 268, 288, 304, 368, 384, 432, 448, 496, 512, and 752, together with all numbers obtained by multiplying these numbers by a power of 4. This gives all known such numbers less than 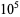 (Savin 2000). All numbers
(Savin 2000). All numbers 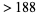 can be expressed as the sum of at most five distinct squares, and only
can be expressed as the sum of at most five distinct squares, and only
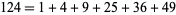 |
(24) |
and
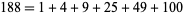 |
(25) |
require six distinct squares (Bohman et al. 1979; Guy 1994, p. 136; Savin 2000). In fact, 188 can also be represented using seven distinct squares:
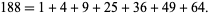 |
(26) |
The following table gives the numbers that can be represented in 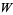 different ways as a sum of
different ways as a sum of 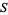 squares. For example,
squares. For example,
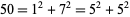 |
(27) |
can be represented in two ways (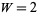 ) by two squares (
) by two squares (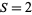 ).
).
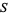 |
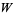 |
Sloane | numbers |
| 1 | 1 | A000290 | 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, ... |
| 2 | 1 | A025284 | 2, 5, 8, 10, 13, 17, 18, 20, 25, 26, 29, 32, ... |
| 2 | 2 | A025285 | 50, 65, 85, 125, 130, 145, 170, 185, 200, ... |
| 3 | 1 | A025321 | 3, 6, 9, 11, 12, 14, 17, 18, 19, 21, 22, 24, ... |
| 3 | 2 | A025322 | 27, 33, 38, 41, 51, 57, 59, 62, 69, 74, 75, ... |
| 3 | 3 | A025323 | 54, 66, 81, 86, 89, 99, 101, 110, 114, 126, ... |
| 3 | 4 | A025324 | 129, 134, 146, 153, 161, 171, 189, 198, ... |
| 4 | 1 | A025357 | 4, 7, 10, 12, 13, 15, 16, 18, 19, 20, 21, 22, ... |
| 4 | 2 | A025358 | 31, 34, 36, 37, 39, 43, 45, 47, 49, 50, 54, ... |
| 4 | 3 | A025359 | 28, 42, 55, 60, 66, 67, 73, 75, 78, 85, 95, 99, ... |
| 4 | 4 | A025360 | 52, 58, 63, 70, 76, 84, 87, 91, 93, 97, 98, 103, ... |
The least numbers that are the sum of two squares in exactly 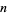 different ways for
different ways for 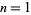 , 2, ... are given by 2, 50, 325, 1105, 8125, 5525, 105625, 27625, 71825, 138125, 5281250, ... (OEIS A016032; Beiler 1966, pp. 140-141; Rubin 1977-78; Culberson 1978-79; Hardy and Wright 1979; Rivera).
, 2, ... are given by 2, 50, 325, 1105, 8125, 5525, 105625, 27625, 71825, 138125, 5281250, ... (OEIS A016032; Beiler 1966, pp. 140-141; Rubin 1977-78; Culberson 1978-79; Hardy and Wright 1979; Rivera).
The product of four distinct nonzero integers in arithmetic progression is square only for (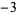 ,
, 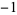 , 1, 3), giving
, 1, 3), giving 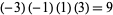 (Le Lionnais 1983, p. 53). It is possible to have three squares in arithmetic progression, but not four (Dickson 2005, pp. 435-440). If these numbers are
(Le Lionnais 1983, p. 53). It is possible to have three squares in arithmetic progression, but not four (Dickson 2005, pp. 435-440). If these numbers are 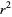 ,
, 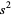 , and
, and 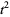 , there are positive integers
, there are positive integers 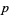 and
and 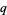 such that
such that
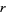 |
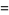 |
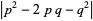 |
(28) |
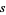 |
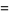 |
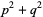 |
(29) |
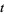 |
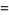 |
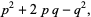 |
(30) |
where 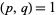 and one of
and one of 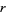 ,
, 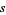 , or
, or 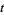 is even (Dickson 2005, pp. 437-438). Every three-term progression of squares can be associated with a Pythagorean triple
is even (Dickson 2005, pp. 437-438). Every three-term progression of squares can be associated with a Pythagorean triple 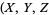 ) by
) by
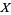 |
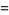 |
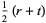 |
(31) |
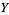 |
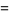 |
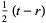 |
(32) |
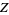 |
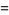 |
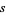 |
(33) |
(Robertson 1996).
Catalan's conjecture states that 8 and 9 (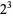 and
and 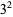 ) are the only consecutive powers (excluding 0 and 1), i.e., the only solution to Catalan's Diophantine problem. This conjecture has not yet been proved or refuted, although R. Tijdeman has proved that there can be only a finite number of exceptions should the conjecture not hold. It is also known that 8 and 9 are the only consecutive cubic and square numbers (in either order).
) are the only consecutive powers (excluding 0 and 1), i.e., the only solution to Catalan's Diophantine problem. This conjecture has not yet been proved or refuted, although R. Tijdeman has proved that there can be only a finite number of exceptions should the conjecture not hold. It is also known that 8 and 9 are the only consecutive cubic and square numbers (in either order).
The numbers that are not the difference of two squares are 2, 6, 10, 14, 18, ... (OEIS A016825; Wells 1986, p. 76).
A square number can be the concatenation of two squares, as in the case 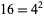 and
and 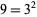 giving
giving 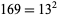 . The first few numbers that are neither square nor the sum of a square and a prime are 10, 34, 58, 85, 91, 130, 214, ... (OEIS A020495).
. The first few numbers that are neither square nor the sum of a square and a prime are 10, 34, 58, 85, 91, 130, 214, ... (OEIS A020495).
It is conjectured that, other than 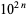 ,
, 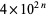 and
and 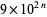 , there are only a finite number of squares
, there are only a finite number of squares 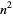 having exactly two distinct nonzero digits (Guy 1994, p. 262). The first few such
having exactly two distinct nonzero digits (Guy 1994, p. 262). The first few such 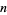 are 4, 5, 6, 7, 8, 9, 11, 12, 15, 21, ... (OEIS A016070), corresponding to
are 4, 5, 6, 7, 8, 9, 11, 12, 15, 21, ... (OEIS A016070), corresponding to 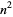 of 16, 25, 36, 49, 64, 81, 121, ... (OEIS A018884).
of 16, 25, 36, 49, 64, 81, 121, ... (OEIS A018884).
The following table gives the first few numbers which, when squared, give numbers composed of only certain digits. The values of 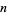 such that
such that 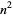 contains exactly two different digits are given by 4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 20, ... (OEIS A016069), whose squares are 16, 25 36, 49, 64, ... (OEIS A018885).
contains exactly two different digits are given by 4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 20, ... (OEIS A016069), whose squares are 16, 25 36, 49, 64, ... (OEIS A018885).
| digits | Sloane | 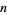 , , 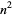 |
| 1, 2, 3 | A030175 | 1, 11, 111, 36361, 363639, ... |
| A030174 | 1, 121, 12321, 1322122321, ... | |
| 1, 4, 6 | A027677 | 1, 2, 4, 8, 12, 21, 38, 108, ... |
| A027676 | 1, 4, 16, 64, 144, 441, 1444, ... | |
| 1, 4, 9 | A027675 | 1, 2, 3, 7, 12, 21, 38, 107, ... |
| A006716 | 1, 4, 9, 49, 144, 441, 1444, 11449, ... | |
| 2, 4, 8 | A027679 | 2, 22, 168, 478, 2878, 210912978, ... |
| A027678 | 4, 484, 28224, 228484, 8282884, ... | |
| 4, 5, 6 | A030177 | 2, 8, 216, 238, 258, 738, 6742, ... |
| A030176 | 4, 64, 46656, 56644, 66564, ... |
For three digits, an extreme example containing only the digits 7, 8, and 9 is
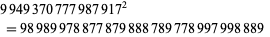 |
(34) |
No squares are known containing only the digits 013 or 678. Unique solutions are known for 019, 039, 056, 079, 568, and 789. The longest known is
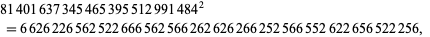 |
(35) |
with 52 digits. A list of known solutions to the 3-digit square problem is maintained by Mishima.
Brown numbers are pairs 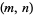 of integers satisfying the condition of Brocard's problem, i.e., such that
of integers satisfying the condition of Brocard's problem, i.e., such that
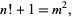 |
(36) |
where 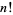 is a factorial. Only three such numbers are known: (5,4), (11,5), (71,7). Erdős conjectured that these are the only three such pairs.
is a factorial. Only three such numbers are known: (5,4), (11,5), (71,7). Erdős conjectured that these are the only three such pairs.
Either 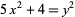 or
or 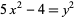 has a solution in positive integers iff, for some
has a solution in positive integers iff, for some 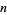 ,
, 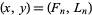 , where
, where 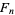 is a Fibonacci number and
is a Fibonacci number and 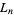 is a Lucas number (Honsberger 1985, pp. 114-118).
is a Lucas number (Honsberger 1985, pp. 114-118).
The smallest and largest square numbers containing the digits 1 to 9 are
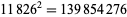 |
(37) |
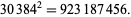 |
(38) |
The smallest and largest square numbers containing the digits 0 to 9 are
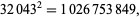 |
(39) |
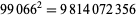 |
(40) |
(Madachy 1979, p. 159). The smallest and largest square numbers containing the digits 1 to 9 twice each are
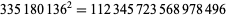 |
(41) |
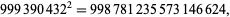 |
(42) |
and the smallest and largest containing 1 to 9 three times are
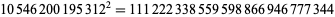 |
(43) |
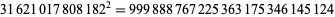 |
(44) |
(Madachy 1979, p. 159).
Madachy (1979, p. 165) also considers numbers that are equal to the sum of the squares of their two "halves" such as
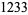 |
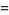 |
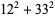 |
(45) |
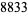 |
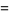 |
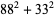 |
(46) |
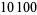 |
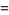 |
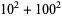 |
(47) |
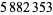 |
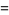 |
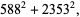 |
(48) |
in addition to a number of others.
REFERENCES:
Archibald, R. G. "Waring's Problem: Squares." Scripta Math. 7, 33-48, 1940.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 59, 1987.
Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.
Bohman, J.; Fröberg, C.-E.; and Riesel, H. "Partitions in Squares." BIT 19, 297-301, 1979.
Cole, C. "rec.puzzles FAQ3." https://www.ifindkarma.com/attic/PUZZLES/rec.puz.faq3.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 30-32 and 146-147, 1996.
Culberson, J. "Solution to Problem 590." J. Recr. Math. 11, 137-138, 1978-79.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, 2005.
Finch, S. "On a Generalized Fermat-Wiles Equation." https://algo.inria.fr/csolve/fermat.pdf.
Grosswald, E. Representations of Integers as Sums of Squares. New York: Springer-Verlag, 1985.
Guy, R. K. "Sums of Squares" and "Squares with Just Two Different Decimal Digits." §C20 and F24 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 136-138, 147, and 262, 1994.
Hajdu, L. and Pintér, Á. "Square Product of Three Integers in Short Intervals." Math. Comput. 68, 1299-1301, 1999.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. "The Representation of a Number by Two or Four Squares." Ch. 20 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 297-316, 1979.
Honsberger, R. "A Second Look at the Fibonacci and Lucas Numbers." Ch. 8 in Mathematical Gems III. Washington, DC: Math. Assoc. Amer., 1985.
Landau, E. "Über die Einteilung der positiven ganzen Zahlen in vier Klassen nach der Mindeszahl der zu ihrer additiven Zusammensetzung erforderlichen Quadrate." Arch. Math. Phys. 13, 305-312, 1908.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983.
Lucas, É. Question 1180. Nouv. Ann. Math. Ser. 2 14, 336, 1875.
Lucas, É. Solution de Question 1180. Nouv. Ann. Math. Ser. 2 15, 429-432, 1876.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 159 and 165, 1979.
Meyl, A.-J.-J. Solution de Question 1194. Nouv. Ann. Math. 17, 464-467, 1878.
Mishima, H. "Sporadic Solutions." https://www.asahi-net.or.jp/~KC2H-MSM/mathland/math02/math0210.htm.
Nagell, T. Introduction to Number Theory. New York: Wiley, 1951.
Ogilvy, C. S. and Anderson, J. T. Excursions in Number Theory. New York: Dover, pp. 77 and 152, 1988.
Pappas, T. "Triangular, Square & Pentagonal Numbers." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 214, 1989.
Pietenpol, J. L. "Square Triangular Numbers." Amer. Math. Monthly 69, 168-169, 1962.
Rivera, C. "Problems & Puzzles: Puzzle 062-The qs-Sequence." https://www.primepuzzles.net/puzzles/puzz_062.htm.
Robertson, J. P. "Magic Squares of Squares." Math. Mag. 69, 289-293, 1996.
Rubin, F. "Problem 590." J. Recr. Math. 10, 46, 1977-78.
Savin, A. "Shape Numbers." Quantum 11, 14-18, 2000.
Sloane, N. J. A. Sequences A000037/M0613, A000290/M3356, A000415, A000419, A001156/M0221, A001422, A001481/M0968, A002828/M0404, A004215/M4349, A006716/M3369, A016069, A016070, A016032, A016825, A018884, A018885, A020495, A025284, A025285, A025321, A025322, A025323, A025324, A025357, A025358, A025359, A025360, A027675, A027676, A027677, A027678, A027679, A030174, A030175, A030176, A030177, A056991, and A056992 in "The On-Line Encyclopedia of Integer Sequences."
Stangl, W. D. "Counting Squares in  ." Math. Mag. 69, 285-289, 1996.
." Math. Mag. 69, 285-289, 1996.
Taussky-Todd, O. "Sums of Squares." Amer. Math. Monthly 77, 805-830, 1970.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 20 and 234-237, 1991.
Watson, G. N. "The Problem of the Square Pyramid." Messenger. Math. 48, 1-22, 1918.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 48 and 70, 1986.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|