


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-6-2021
Date: 3-8-2021
Date: 28-9-2016
|
 |
 |
The stevedore's knot is the 6-crossing prime knot 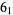 . It is implemented in the Wolfram Language as KnotData["Stevedore"].
. It is implemented in the Wolfram Language as KnotData["Stevedore"].
It has braid word 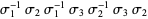 . It has Arf invariant 0 and is not amphichiral, although it is invertible. It is a slice knot (Rolfsen 1976, p. 225).
. It has Arf invariant 0 and is not amphichiral, although it is invertible. It is a slice knot (Rolfsen 1976, p. 225).
The Alexander polynomial 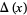 , BLM/Ho polynomial
, BLM/Ho polynomial 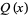 , Conway polynomial
, Conway polynomial 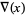 , HOMFLY polynomial
, HOMFLY polynomial 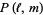 , and Jones polynomial
, and Jones polynomial 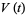 of Stevedore's knot are
of Stevedore's knot are
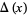 |
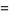 |
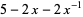 |
(1) |
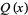 |
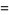 |
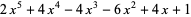 |
(2) |
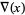 |
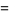 |
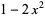 |
(3) |
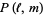 |
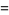 |
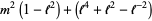 |
(4) |
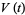 |
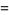 |
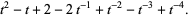 |
(5) |
Surprisingly, the knot 09-046 shares the same Alexander polynomial with the stevedore's knot. However, no knots on 10 or fewer crossings share the same BLM/Ho polynomial or Jones polynomial with it.
REFERENCES:
Bar-Natan, D. "The Knot 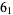 ." https://www.math.toronto.edu/~drorbn/KAtlas/Knots/6.1.html.
." https://www.math.toronto.edu/~drorbn/KAtlas/Knots/6.1.html.
KnotPlot. "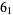 ." https://newweb.cecm.sfu.ca/cgi-bin/KnotPlot/KnotServer/kserver?ncomp=1&ncross=6&id=1.
." https://newweb.cecm.sfu.ca/cgi-bin/KnotPlot/KnotServer/kserver?ncomp=1&ncross=6&id=1.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, p. 225, 1976.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|