Pyramidal Number

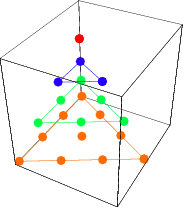
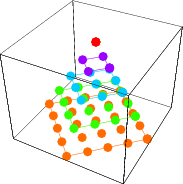
A figurate number corresponding to a configuration of points which form a pyramid with 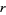-sided regular polygon bases can be thought of as a generalized pyramidal number, and has the form

(1)

The first few cases are therefore

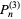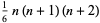			(2)
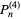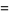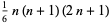			(3)
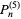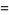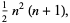			(4)

so 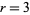 corresponds to a tetrahedral number 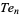, and 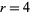 to a square pyramidal number .

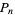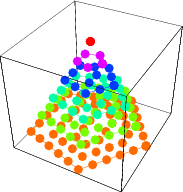
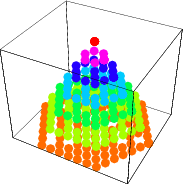
The pyramidal numbers can also be generalized to four dimensions and higher dimensions (Sloane and Plouffe 1995).

REFERENCES:

Conway, J. H. and Guy, R. K. "Tetrahedral Numbers" and "Square Pyramidal Numbers" The Book of Numbers. New York: Springer-Verlag, pp. 44-49, 1996.

Sloane, N. J. A. and Plouffe, S. "Pyramidal Numbers." Extended entry for sequence M3382 in The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, 1995.