Andrica's conjecture states that, for 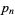 the 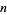th prime number, the inequality

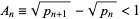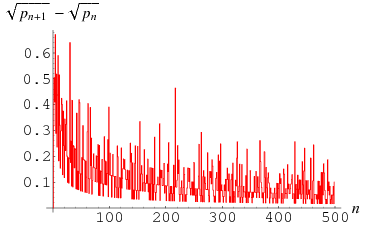
holds, where the discrete function 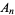 is plotted above. The high-water marks for  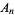occur for 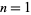, 2, and 4, with 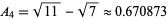, with no larger value among the first  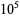primes. Since the Andrica function falls asymptotically as  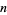increases, a prime gap of ever increasing size is needed to make the difference large as  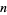becomes large. It therefore seems highly likely the conjecture is true, although this has not yet been proven.

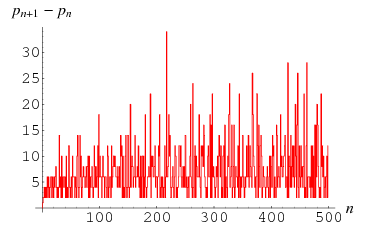
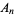 bears a strong resemblance to the prime difference function, plotted above, the first few values of which are 1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, ... (OEIS A001223).

A generalization of Andrica's conjecture considers the equation

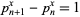and solves for . The smallest such  is 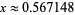 (OEIS A038458), known as the Smarandache constant, which occurs for  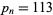and 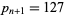 (Perez).

REFERENCES:

Andrica, D. "Note on a Conjecture in Prime Number Theory." Studia Univ. Babes-Bolyai Math. 31, 44-48, 1986.

Golomb, S. W. "Problem E2506: Limits of Differences of Square Roots." Amer. Math. Monthly 83, 60-61, 1976.

Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 21, 1994.

Perez, M. L. (Ed.). "Five Smarandache Conjectures on Primes." https://www.gallup.unm.edu/~smarandache/conjprim.txt.

Rivera, C. "Problems & Puzzles: Conjecture 008.-Andrica's Conjecture." https://www.primepuzzles.net/conjectures/conj_008.htm.

Sloane, N. J. A. Sequences A001223/M0296 and A038458 in "The On-Line Encyclopedia of Integer Sequences."

Wells, D. Prime Numbers: The Most Mysterious Figures in Math. New York: Wiley, p. 13, 2005.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد