


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-11-2019
Date: 21-1-2021
Date: 11-11-2020
|
A number which is simultaneously octagonal and triangular. Let 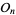 denote the
denote the 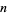 th octagonal number and
th octagonal number and 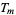 the
the 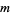 th triangular number, then a number which is both octagonal and triangular satisfies the equation
th triangular number, then a number which is both octagonal and triangular satisfies the equation 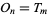 , or
, or
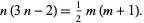 |
(1) |
Completing the square and rearranging gives
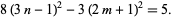 |
(2) |
Therefore, defining
 |
 |
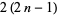 |
(3) |
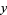 |
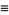 |
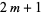 |
(4) |
gives the second-order Diophantine equation
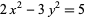 |
(5) |
The first few solutions are 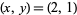 , (4, 3), (16, 13), (38, 31), (158, 129), (376, 307), .... These give the solutions
, (4, 3), (16, 13), (38, 31), (158, 129), (376, 307), .... These give the solutions 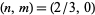 , (1, 1), (3, 6), (20/3, 15), (80/3, 64), (63, 153), ..., of which the integer solutions are (1, 1), (3, 6), (63, 153), (261, 638), (6141, 15041), (25543, 62566), (601723, 1473913), ... (OEIS A046181 and A046182), corresponding to the octagonal triangular numbers 1, 21, 11781, 203841, 113123361, ... (OEIS A046183).
, (1, 1), (3, 6), (20/3, 15), (80/3, 64), (63, 153), ..., of which the integer solutions are (1, 1), (3, 6), (63, 153), (261, 638), (6141, 15041), (25543, 62566), (601723, 1473913), ... (OEIS A046181 and A046182), corresponding to the octagonal triangular numbers 1, 21, 11781, 203841, 113123361, ... (OEIS A046183).
REFERENCES:
Sloane, N. J. A. Sequences A046181, A046182, and A046183 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
الصين.. طريقة لمنع تطور قصر النظر لدى تلاميذ المدارس
|
|
|
|
|
|
|
ماذا سيحدث خلال كسوف الشمس يوم السبت؟
|
|
|
|
|
|
|
بمشاركة مجتمعيّة واسعة .. اختتام فعاليات المجلس العلوي الثقافي السنوي الثاني
|
|
|