Gelfand,s Question
المؤلف:
Avez, A.
المصدر:
Ergodic Theory of Dynamical Systems, Vol. 1. Minneapolis, MX: University of Minnesota Institute of Technology, 1966.
الجزء والصفحة:
...
11-11-2020
1013
Gelfand's Question
 |
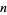Sloane's |
 |
 |
 |
 |
 |
 |
 |
 |
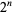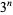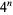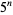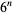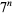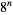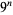| 1 |
A000027 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 2 |
A002993 |
4 |
9 |
1 |
2 |
3 |
4 |
6 |
8 |
| 3 |
A002994 |
8 |
2 |
6 |
1 |
2 |
3 |
5 |
7 |
| 4 |
A097408 |
1 |
8 |
2 |
6 |
1 |
2 |
4 |
6 |
| 5 |
A097409 |
3 |
2 |
1 |
3 |
7 |
1 |
3 |
5 |
| 6 |
A097410 |
6 |
7 |
4 |
1 |
4 |
1 |
2 |
5 |
| 7 |
A097411 |
1 |
2 |
1 |
7 |
2 |
8 |
2 |
4 |
| 8 |
A097412 |
2 |
6 |
6 |
3 |
1 |
5 |
1 |
4 |
| 9 |
A097413 |
5 |
1 |
2 |
1 |
1 |
4 |
1 |
3 |
| 10 |
A097414 |
1 |
5 |
1 |
9 |
6 |
2 |
1 |
3 |
Consider the leftmost (i.e., most significant) decimal digit of the numbers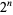 
, 
, ..., 
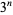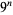. Then what are the patterns of digits occurring in the table for 
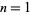, 2, ... (King 1994)? For example,
1. Will the digit 9 ever occur in the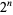 
column? The answer is "yes," in particular at values 
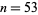, 63, 73, 83, 93, 156, 166, 176, ... (OEIS A097415. This problem appears in Avez (1966, p. 37), where it is attributed to Gelfand.
2. Will the row "23456789" ever appear for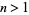 
? None does for 
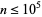. If so, will it have a frequency? If so, will the frequency be rational or irrational?
3. Will a row of all the same digit occur? No such example occurs for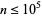 
.
4. Will the decimal expansion of an 8-digit prime ever occur? (The answer is "yes," in particular at values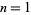 
, 11, 21, 44, 55, 81, 90, 118, 126, ... (OEIS A097616), corresponding to the primes 23456789, 21443183, 21442591, 19351159, ... (OEIS A097617).
Amazingly, this problem is isomorphic to Poncelet's porism (King 1994).
REFERENCES:
Avez, A. Ergodic Theory of Dynamical Systems, Vol. 1. Minneapolis, MX: University of Minnesota Institute of Technology, 1966.
King, J. L. "Three Problems in Search of a Measure." Amer. Math. Monthly 101, 609-628, 1994.
Previato, E. "Featured Review: CRC Concise Encyclopedia of Mathematics. Second Edition." SIAM Rev. 46, 349-354, 2004.
Sloane, N. J. A. Sequences A000027/M0472, A002993/M3348, A002994/M4468, A097408, A097409, A097410, A097411, A097412, A097413, A097414, A097415, A097616, and A097617 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
