A problem posed by L. Collatz in 1937, also called the 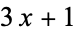 mapping,  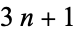problem, Hasse's algorithm, Kakutani's problem, Syracuse algorithm, Syracuse problem, Thwaites conjecture, and Ulam's problem (Lagarias 1985). Thwaites (1996) has offered a £1000 reward for resolving the conjecture. Let  be an integer. Then one form of Collatz problem asks if iterating

(1)

always returns to 1 for positive 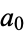. (If negative numbers are included, there are four known cycles (excluding the trivial 0 cycle): (4, 2, 1), (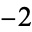, 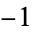), (, 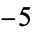, , 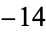, 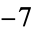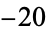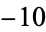), and (, , , , , , , , , , , , , , , , , ).)

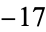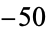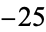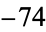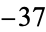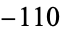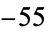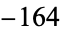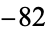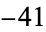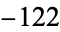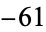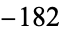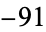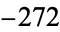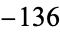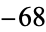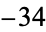The members of the sequence produced by the Collatz are sometimes known as hailstone numbers. Conway proved that the original Collatz problem has no nontrivial cycles of length 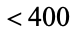. Lagarias (1985) showed that there are no nontrivial cycles with length 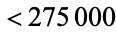. Conway (1972) also proved that Collatz-type problems can be formally undecidable. Kurtz and Simon (2007) proved that a natural generalization of the Collatz problem is undecidable; unfortunately, this proof cannot be applied to the original Collatz problem.

The Collatz algorithm has been tested and found to always reach 1 for all numbers 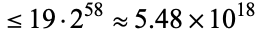 (Oliveira e Silva 2008), improving the earlier results of  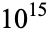(Vardi 1991, p. 129) and  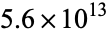(Leavens and Vermeulen 1992). Because of the difficulty in solving this problem, Erdős commented that "mathematics is not yet ready for such problems" (Lagarias 1985).

The following table gives the sequences obtained for the first few starting values (OEIS A070165).

	, , , ...
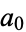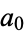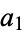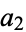1	1
2	2, 1
3	3, 10, 5, 16, 8, 4, 2, 1
4	4, 2, 1
5	5, 16, 8, 4, 2, 1
6	6, 3, 10, 5, 16, 8, 4, 2, 1

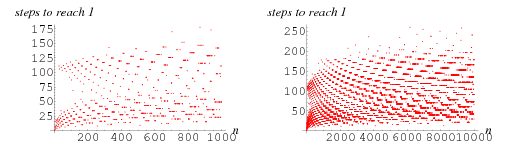
The numbers of steps required for the algorithm to reach 1 for 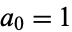, 2, ... are 0, 1, 7, 2, 5, 8, 16, 3, 19, 6, 14, 9, 9, 17, 17, 4, 12, 20, 20, 7, ... (OEIS A006577; illustrated above). Of these, the numbers of tripling steps are 0, 0, 2, 0, 1, 2, 5, 0, 6, ... (OEIS A006667), and the number of halving steps are 0, 1, 5, 2, 4, 6, 11, 3, 13, ... (OEIS A006666). The smallest starting values of  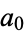that yields a Collatz sequence containing 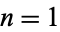, 2, ... are 1, 2, 3, 3, 3, 6, 7, 3, 9, 3, 7, 12, 7, 9, 15, 3, 7, 18, 19, ... (OEIS A070167).

The Collatz problem can be implemented as an 8-register machine (Wolfram 2002, p. 100), quasi-cellular automaton (Cloney et al. 1987, Bruschi 2005), or 6-color one-dimensional quasi-cellular automaton with local rules but which wraps first and last digits around (Zeleny). In general, the difficulty in constructing true local-rule cellular automata arises from the necessity of a carry operation when multiplying by 3 which, in the worst case, can extend the entire length of the base-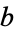 representation of digits (and thus require propagating information at faster than the CA's speed of light).

The Collatz problem was modified by Terras (1976, 1979), who asked if iterating

(2)

always returns to 1 for initial integer value 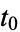 (e.g., Lagarias 1985, Cloney et al. 1987). This is simply the original statement above but combining the division by two into the addition step if  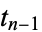is odd, thus compressing the number of steps. The following table gives the sequences for the first few starting values 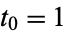, 2, ... (OEIS A070168).

	, , ...
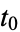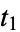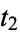1	1
2	2, 1
3	3, 5, 8, 4, 2, 1
4	4, 2, 1
5	5, 8, 4, 2, 1
6	6, 3, 5, 8, 4, 2, 1
7	7, 11, 17, 26, 13, 20, 10, 5, 8, 4, 2, 1

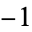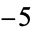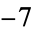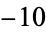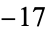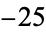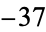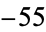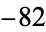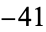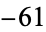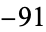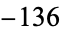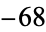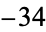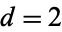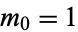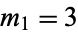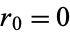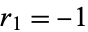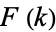If negative numbers are included, there are 4 known cycles: (1, 2), (), (, , ), and (, , , , , , , , , , ). It is a special case of the "generalized Collatz problem" with , , , , and . Terras (1976, 1979) also proved that the set of integers  has a limiting asymptotic density , such that if  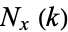is the number of  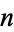such that  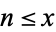and 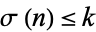, then the limit

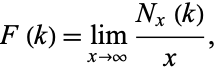(3)

exists. Furthermore, 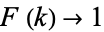 as 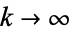, so almost all integers have a finite stopping time. Finally, for all ,

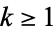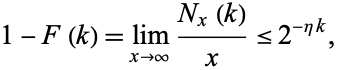(4)

where

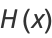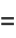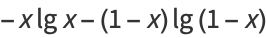			(5)
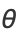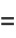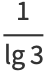			(6)
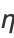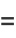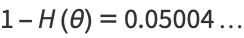			(7)

(Lagarias 1985).

A generalization of the Collatz problem lets 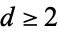 be a positive integer and 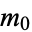, ...,  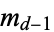be nonzero integers. Also let  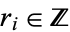satisfy

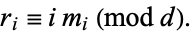(8)

Then

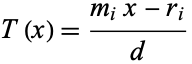(9)

for 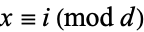 defines a generalized Collatz mapping. An equivalent form is

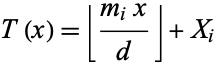(10)

for 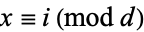 where 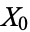, ...,  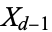are integers and  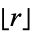is the floor function. The problem is connected with ergodic theory and Markov chains. Matthews obtained the following table for the mapping

(11)

where .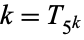

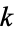	# cycles	max. cycle length
0	5	27
1	10	34
2	13	118
3	17	118
4	19	118
5	21	165
6	23	433

Matthews and Watts (1984) proposed the following conjectures.

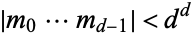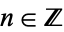1. If , then all trajectories  for  eventually cycle.

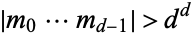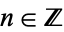2. If , then almost all trajectories  for  are divergent, except for an exceptional set of integers  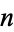satisfying

(12)

3. The number of cycles is finite.

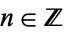4. If the trajectory  for  is not eventually cyclic, then the iterates are uniformly distribution mod  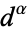for each 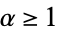, with

(13)

for .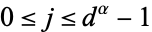

Matthews believes that the map

(14)

will either reach 0 (mod 3) or will enter one of the cycles 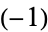 or 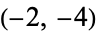, and offers a $100 (Australian?) prize for a proof.

REFERENCES:

Applegate, D. and Lagarias, J. C. "Density Bounds for the 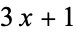 Problem 1. Tree-Search Method." Math. Comput. 64, 411-426, 1995.

Applegate, D. and Lagarias, J. C. "Density Bounds for the 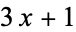 Problem 2. Krasikov Inequalities." Math. Comput. 64, 427-438, 1995.

Bruschi, M. "Two Cellular Automata for the 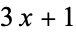 Map." https://arxiv.org/abs/nlin/0502061/. 26 Feb, 2005.

Burckel, S. "Functional Equations Associated with Congruential Functions." Theor. Comp. Sci. 123, 397-406, 1994.

Cloney, T.; Goles, E.; and Vichniac, G. Y. "The 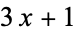 Problem: A Quasi Cellular Automaton." Complex Sys. 1, 349-360, 1987.

Conway, J. H. "Unpredictable Iterations." Proc. 1972 Number Th. Conf., University of Colorado, Boulder, Colorado, pp. 49-52, 1972.

Crandall, R. "On the '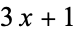' Problem." Math. Comput. 32, 1281-1292, 1978.

De Mol, L. "Tag Systems and Collatz-Like Functions." Theor. Comput. Sci. 390, 92-101, 2008.

Everett, C. "Iteration of the Number Theoretic Function 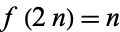, 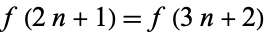." Adv. Math. 25, 42-45, 1977.

Guy, R. K. "Collatz's Sequence." §E16 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 215-218, 1994.

Kurtz, S. A. and Simon, J. "The Undecidability of the Generalized Collatz Problem." In Theory and Applications of Models of Computation: Proceedings of the 4th International Conference (TAMC 2007) held in Shanghai, May 22-25, 2007 (Ed. J.-Y. Cai, S. B. Cooper, and H. Zhu). Berlin: Springer, pp. 542-553, 2007.

Lagarias, J. C. "The 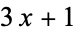 Problem and Its Generalizations." Amer. Math. Monthly 92, 3-23, 1985.

Leavens, G. T. and Vermeulen, M. "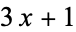 Search Programs." Comput. Math. Appl. 24, 79-99, 1992.

Margenstern, M. and Matiyasevich, Y. "A Binomial Representation of the 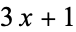 Problem." Acta Arith. 91, 367-378, 1999.

Matthews, K. R. "The Generalized 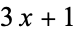 Mapping." https://www.numbertheory.org/pdfs/survey.pdf.

Matthews, K. R. "A Generalized 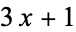 Conjecture." [$100 Reward for a Proof.] https://www.numbertheory.org/gnubc/challenge.

Matthews, K. R. and Watts, A. M. "A Generalization of Hasses's Generalization of the Syracuse Algorithm." Acta Arith. 43, 167-175, 1984.

Oliveira e Silva, T. "Maximum Excursion and Stopping Time Record-Holders for the 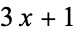 Problem: Computational Results." Math. Comput. 68, 371-384, 1999.

Oliveira e Silva, T. "Computational Verification of the 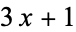 Conjecture." Sep. 19, 2008. https://www.ieeta.pt/~tos/3x+1.html.

Schroeppel, R.; Gosper, R. W.; Henneman, W.; and Banks, R. Item 133 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 64, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/flows.html#item133.

Sloane, N. J. A. Sequences A006577/M4323, A006666/M3733, A006667/M0019, A070165, A070166, A070167, A070168, in "The On-Line Encyclopedia of Integer Sequences."

Terras, R. "A Stopping Time Problem on the Positive Integers." Acta Arith. 30, 241-252, 1976.

Terras, R. "On the Existence of a Density." Acta Arith. 35, 101-102, 1979.

Thwaites, B. "Two Conjectures, or How to Win £1100." Math. Gaz. 80, 35-36, 1996.

Vardi, I. "The 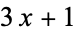 Problem." Ch. 7 in Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 129-137, 1991.

Wirsching, G. J. "Über das 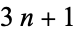 Problem." Elem. Math. 55, 142-155, 2000.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 100, 122, and 904, 2002.

Zeleny, E. "Collatz Problem as a Cellular Automaton." https://demonstrations.wolfram.com/CollatzProblemAsACellularAutomaton/.