Perfect numbers are positive integers 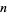 such that

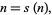(1)

where 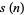 is the restricted divisor function (i.e., the sum of proper divisors of 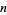), or equivalently

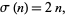(2)

where 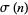 is the divisor function (i.e., the sum of divisors of  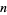including  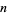itself). For example, the first few perfect numbers are 6, 28, 496, 8128, ... (OEIS A000396), since

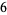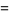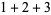			(3)
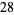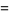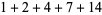			(4)
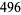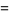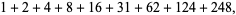			(5)

etc.

The 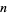th perfect number is implemented in the Wolfram Language as PerfectNumber[n] and checking to see if  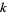is a perfect number as PerfectNumberQ[k].

The first few perfect numbers 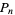 are summarized in the following table together with their corresponding indices  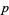(see below).

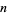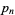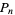1	2	6
2	3	28
3	5	496
4	7	8128
5	13	33550336
6	17	8589869056
7	19	137438691328
8	31	2305843008139952128

Perfect numbers were deemed to have important numerological properties by the ancients, and were extensively studied by the Greeks, including Euclid.

Perfect numbers are also intimately connected with a class of numbers known as Mersenne primes, which are prime numbers of the form 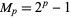. This can be demonstrated by considering a perfect number  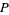of the form  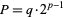where 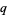 is prime. By definition of a perfect number ,

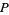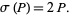(6)

Now note that there are special forms for the divisor function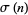 

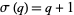(7)

for 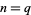 a prime, and

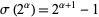(8)

for 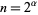. Combining these with the additional identity

(9)

where 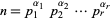 is the prime factorization of 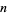, gives

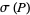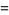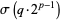			(10)
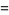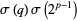			(11)
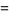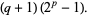			(12)

But 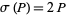, so

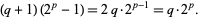(13)

Solving for 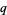 then gives

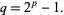(14)

Therefore, if 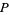 is to be a perfect number,  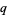must be of the form 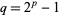. Defining  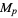as a prime number of the form 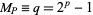, it then follows that

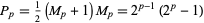(15)

is a perfect number, as stated in Proposition IX.36 of Euclid's Elements (Dickson 2005, p. 3; Dunham 1990).

While many of Euclid's successors implicitly assumed that all perfect numbers were of the form (15) (Dickson 2005, pp. 3-33), the precise statement that all even perfect numbers are of this form was first considered in a 1638 letter from Descartes to Mersenne (Dickson 2005, p. 12). Proof or disproof that Euclid's construction gives all possible even perfect numbers was proposed to Fermat in a 1658 letter from Frans van Schooten (Dickson 2005, p. 14). In a posthumous 1849 paper, Euler provided the first proof that Euclid's construction gives all possible even perfect numbers (Dickson 2005, p. 19).

It is not known if any odd perfect numbers exist, although numbers up to 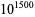 (Ochem and Rao 2012) have been checked without success.

All even perfect numbers  are of the form

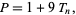(16)

where 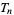 is a triangular number

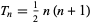(17)

such that 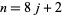 (Eaton 1995, 1996). In addition, all even perfect numbers are hexagonal numbers, so it follows that even perfect numbers are always the sum of consecutive positive integers starting at 1, for example,

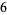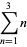			(18)
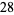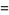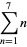			(19)
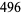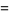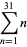			(20)

(Singh 1997), where 3, 7, 31, ... (OEIS A000668) are simply the Mersenne primes. In addition, every even perfect number 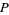 is of the form 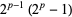, so they can be generated using the identity

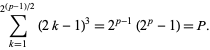(21)

It is known that all even perfect numbers (except 6) end in 16, 28, 36, 56, 76, or 96 (Lucas 1891) and have digital root 1. In particular, the last digits of the first few perfect numbers are 6, 8, 6, 8, 6, 6, 8, 8, 6, 6, 8, 8, 6, 8, 8, ... (OEIS A094540), where the region between the 38th and 41st terms has been incompletely searched as of June 2004.

The sum of reciprocals of all the divisors of a perfect number is 2, since

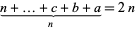(22)

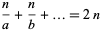(23)

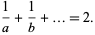(24)

If 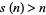,  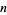is said to be an abundant number. If 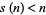,  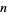is said to be a deficient number. And if  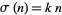for a positive integer 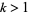,  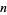is said to be a multiperfect number of order .

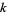The only even perfect number of the form 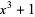 is 28 (Makowski 1962).

Ruiz has shown that 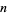 is a perfect number iff

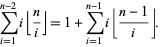(25)

REFERENCES:

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 66-67, 1987.

Brent, R. P.; Cohen, G. L. L.; and te Riele, H. J. J. "Improved Techniques for Lower Bounds for Odd Perfect Numbers." Math. Comput. 57, 857-868, 1991.

Conway, J. H. and Guy, R. K. "Perfect Numbers." In The Book of Numbers. New York: Springer-Verlag, pp. 136-137, 1996.

Dickson, L. E. "Notes on the Theory of Numbers." Amer. Math. Monthly 18, 109-111, 1911.

Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 3-33, 2005.

Dunham, W. Journey through Genius: The Great Theorems of Mathematics. New York: Wiley, p. 75, 1990.

Eaton, C. F. "Problem 1482." Math. Mag. 68, 307, 1995.

Eaton, C. F. "Perfect Number in Terms of Triangular Numbers." Solution to Problem 1482. Math. Mag. 69, 308-309, 1996.

Gardner, M. "Perfect, Amicable, Sociable." Ch. 12 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 160-171, 1978.

Guy, R. K. "Perfect Numbers." §B1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 44-45, 1994.

Iannucci, D. E. "The Second Largest Prime Divisor of an Odd Perfect Number Exceeds Ten Thousand." Math. Comput. 68, 1749-1760, 1999.

Kraitchik, M. "Mersenne Numbers and Perfect Numbers." §3.5 in Mathematical Recreations. New York: W. W. Norton, pp. 70-73, 1942.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 145 and 147-151, 1979.

Makowski, A. "Remark on Perfect Numbers." Elemente Math. 17, 109, 1962.

McDaniel, W. L. "On the Proof That All Even Perfect Numbers Are of Euclid's Type." Math. Mag. 48, 107-108, 1975.

Ochem, P. and Rao, M. "Odd Perfect Numbers Are Greater than 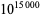." Math. Comput. 81, 1869-1877, 2012.

Powers, R. E. "The Tenth Perfect Number." Amer. Math. Monthly 18, 195-196, 1911.

Séroul, R. "Perfect Numbers." §8.3 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 163-165, 2000.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 1-13 and 25-29, 1993.

Singh, S. Fermat's Enigma: The Epic Quest to Solve the World's Greatest Mathematical Problem. New York: Walker, pp. 11-13, 1997.

Sloane, N. J. A. Sequences A000396/M4186, A000668/M2696, and A094540 in "The On-Line Encyclopedia of Integer Sequences."

Smith, H. J. "Perfect Numbers." https://www.geocities.com/hjsmithh/Perfect.html.

Spira, R. "The Complex Sum of Divisors." Amer. Math. Monthly 68, 120-124, 1961.

Souissi, M. Un Texte Manuscrit d'Ibn Al-Bannā' Al-Marrakusi sur les Nombres Parfaits, Abondants, Deficients, et Amiables. Karachi, Pakistan: Hamdard Nat. Found., 1975.

Wagon, S. "Perfect Numbers." Math. Intell. 7, 66-68, 1985.

Zachariou, A. and Zachariou, E. "Perfect, Semi-Perfect and Ore Numbers." Bull. Soc. Math. Grèce (New Ser.) 13, 12-22, 1972.