OBSERVATIONAL CONFIRMATION

When Einstein developed his general theory of relativity, some of the paradoxes inherent in special relativity were resolved. (These paradoxes have been avoided here because discussing them would only confuse you.) In particular, light rays from distant stars were observed as they passed close to the Sun to see whether or not the Sun’s gravitational field, which is quite strong near its surface, would bend the light rays. This bending would be observed as a change in the apparent position of a distant star in the sky as the Sun passes close to it (Fig. 1).
The problem with this type of observation was, as you might guess, the fact that the Sun is far brighter than any other star in the sky, and the Sun’s light normally washes out the faint illumination from distant stars.
However, during a total solar eclipse, the Sun’s disk is occulted by the Moon. In addition, the angular diameter of the Moon in the sky is almost exactly the same as that of the Sun, so light from distant stars passing close to the Sun can be seen by earthbound observers during a total eclipse. When this experiment was carried out, the apparent position of a distant star was indeed offset by the presence of the Sun, and this effect took place to the same extent as Einstein’s general relativity formulas said it should.

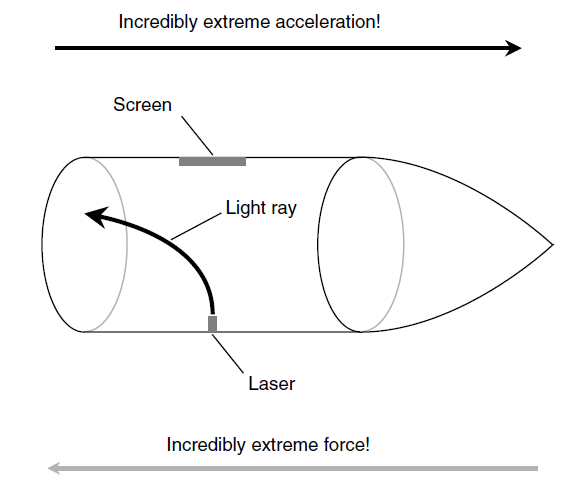
Fig. 1. If the acceleration is great enough, the spatial curvature becomes extreme.

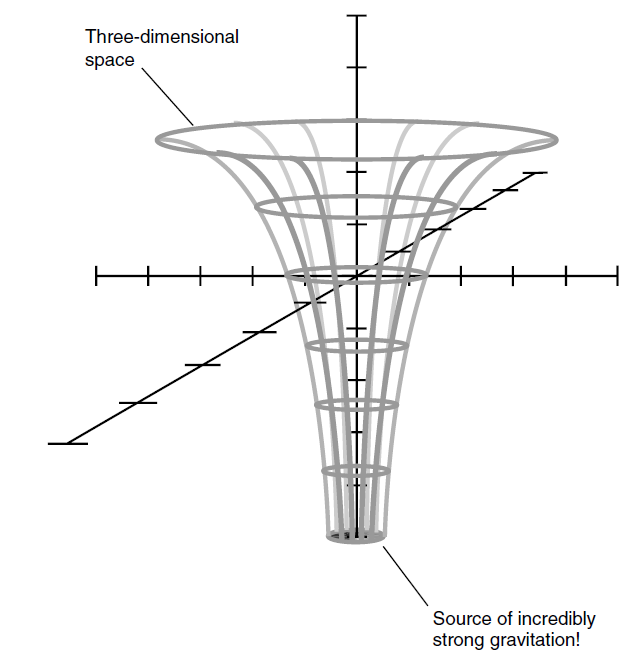
Fig. 2. Spatial curvature in the vicinity of an object that produces an intense gravitational field.

More recently, the light from a certain quasar has been observed as it passes close to a suspected black hole. On its way to us, the light from the quasar follows multiple curved paths around the dark, massive object. This produces several images of the quasar, arranged more or less in the form of a “plus sign” or “cross” with the dark object at the center.
The curvature of space in the presence of a strong gravitational field has been likened to a funnel shape (Fig. 2), except that the surface of the funnel is three-dimensional rather than two-dimensional. The shortest distance in three-dimensional space between any two points near the gravitational source is always a curve with respect to four-dimensional space. This is impossible for most (if not all) people to envision directly without “cheating” by taking away one dimension. The mathematics is straightforward enough, though, and observations have shown that it correctly explains the phenomenon.