
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-11-2019
Date: 19-8-2020
Date: 1-8-2020
|
A number which is simultaneously a nonagonal number 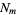 and a square number
and a square number 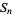 and therefore satisfies the Diophantine equation
and therefore satisfies the Diophantine equation
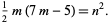 |
(1) |
Completing the square and rearranging gives
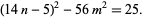 |
(2) |
Defining 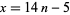 and
and 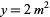 gives the Pell-like equation
gives the Pell-like equation
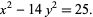 |
(3) |
This has unit solutions 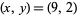 , (23, 6), and (75, 20), which lead to the family of solutions (9, 2), (23, 6), (75, 20), (247, 66), (681, 182), (2245, 600), .... The corresponding integer solutions in
, (23, 6), and (75, 20), which lead to the family of solutions (9, 2), (23, 6), (75, 20), (247, 66), (681, 182), (2245, 600), .... The corresponding integer solutions in 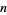 and
and 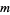 are
are 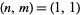 , (2, 3), (18, 33), (49, 91), (529, 989), ... (OEIS A048910 and A048911), giving the nonagonal square numbers 1, 9, 1089, 8281, 978121, 7436529, ... (OEIS A036411).
, (2, 3), (18, 33), (49, 91), (529, 989), ... (OEIS A048910 and A048911), giving the nonagonal square numbers 1, 9, 1089, 8281, 978121, 7436529, ... (OEIS A036411).
REFERENCES:
Sloane, N. J. A. Sequences A048910, A048911, and A036411 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|