Graham's Number

Let 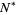 be the smallest dimension  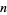of a hypercube such that if the lines joining all pairs of corners are two-colored for any 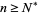, a complete graph  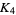of one color with coplanar vertices will be forced. Stated colloquially, this definition is equivalent to considering every possible committee from some number of people  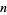and enumerating every pair of committees. Now assign each pair of committees to one of two groups, and find  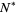the smallest  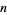that will guarantee that there are four committees in which all pairs fall in the same group and all the people belong to an even number of committees (Hoffman 1998, p. 54).

An answer was proved to exist by Graham and Rothschild (1971), who also provided the best known upper bound, given by

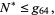(1)

where Graham's number 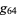 is recursively defined by

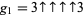(2)

and

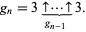(3)

Here,  is the so-called Knuth up-arrow notation. 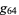 is often cited as the largest number that has ever been put to practical use (Exoo 2003).

In chained arrow notation, 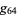 satisfies the inequality

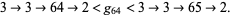(4)

Graham and Rothschild (1971) also provided a lower limit by showing that 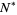 must be at least 6. More recently, Exoo (2003) has shown that  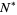must be at least 11 and provides experimental evidence suggesting that it is actually even larger.

REFERENCES:

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 61-62, 1996.

Exoo, G. "A Euclidean Ramsey Problem." Disc. Comput. Geom. 29, 223-227, 2003.

Exoo, G. "A Ramsay Problem on Hypercubes." https://isu.indstate.edu/ge/GEOMETRY/cubes.html.

Gardner, M. "Mathematical Games." Sci. Amer. 237, 18-28, Nov. 1977.

Graham, R. L. and Rothschild, B. L. "Ramsey's Theorem for 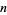-Parameter Sets." Trans. Amer. Math. Soc. 159, 257-292, 1971.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 200 and 209, 2003.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, pp. 18 and 54, 1998.