Convergent Sequence
المؤلف:
Jeffreys, H. and Jeffreys, B. S.
المصدر:
"Bounded, Unbounded, Convergent, Oscillatory." §1.041 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press
الجزء والصفحة:
...
25-10-2020
978
Convergent Sequence
A sequence is said to be convergent if it approaches some limit (D'Angelo and West 2000, p. 259).
Formally, a sequence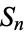 
converges to the limit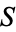 
if, for any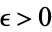 
, there exists an 
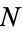such that 
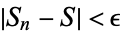for 
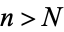. If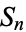 
does not converge, it is said to diverge. This condition can also be written as
Every bounded monotonic sequence converges. Every unbounded sequence diverges.
REFERENCES:
D'Angelo, J. P. and West, D. B. Mathematical Thinking: Problem-Solving and Proofs, 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 2000.
Jeffreys, H. and Jeffreys, B. S. "Bounded, Unbounded, Convergent, Oscillatory." §1.041 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 11-12, 1988.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
