


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-10-2019
Date: 29-8-2020
Date: 12-1-2021
|
Let 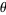 be an irrational number, define
be an irrational number, define 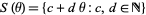 , and let
, and let 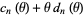 be the sequence obtained by arranging the elements of
be the sequence obtained by arranging the elements of 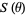 in increasing order. A sequence
in increasing order. A sequence  is said to be a signature sequence if there exists a positive irrational number
is said to be a signature sequence if there exists a positive irrational number 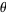 such that
such that 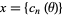 , and
, and  is called the signature of
is called the signature of 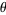 .
.
One can also define two extended signature sequences for positive rational 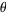 by taking the
by taking the 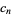 in increasing order or decreasing order. These can be considered signature sequences for
in increasing order or decreasing order. These can be considered signature sequences for 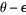 and
and 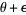 , respectively, where
, respectively, where 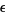 is an infinitesimal.
is an infinitesimal.
The signature of an irrational number or either signature of a rational number is a fractal sequence. Also, if  is a signature or extended signature sequence, then the lower-trimmed subsequence is
is a signature or extended signature sequence, then the lower-trimmed subsequence is 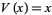 . It has been conjectured that every sequence with both of these properties is a signature or extended signature sequence.
. It has been conjectured that every sequence with both of these properties is a signature or extended signature sequence.
If every initial subsequence of a sequence 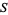 is an initial subsequence of some signature sequence, then
is an initial subsequence of some signature sequence, then 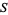 is either a signature sequence, an extended signature sequence, or one of the two limiting cases: all 1's, or the natural numbers (which could be regarded as signature sequences for zero and infinity).
is either a signature sequence, an extended signature sequence, or one of the two limiting cases: all 1's, or the natural numbers (which could be regarded as signature sequences for zero and infinity).
REFERENCES:
Kimberling, C. "Fractal Sequences and Interspersions." Ars Combin. 45, 157-168, 1997.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|