Circular Prime

A prime number 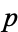 is called circular if it remains prime after any cyclic permutation of its digits. An example in base-10 is  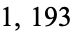because 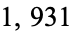, , 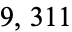and 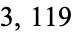 are all primes. The first few circular primes are 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, 97, 113, 131, 197, ... (OEIS A068652).

Base-10 circular primes not contain any digit 0, 2, 4, 5, 6, or 8, since having such a digit in the units place yields a number which is necessarily divisible by eithe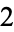r  or 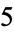 (and therefore not prime).

Every prime repunit is a circular prime.

Circular primes are rare. Including only the smallest number corresponding to each cycle gives the sequence 2, 3, 5, 7, 11, 13, 17, 37, 79, 113, 197, 199, 337, 1193, 3779, 11939, 19937, 193939, 199933, ... (OEIS A016114; Darling 2004), together with repunits 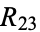, , 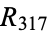, , 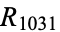, , 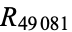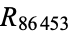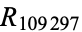and 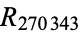 (the last several of which are probable primes).

REFERENCES:

Caldwell, C. "Circular Prime." https://primes.utm.edu/glossary/xpage/CircularPrime.html.

Darling, D. The Universal Book of Mathematics from Abracadabra to Zeno's Paradoxes. Hoboken, NJ: Wiley, 2004.

De Geest, P. "Circular Primes." 2011. https://www.worldofnumbers.com/circular.htm.

Sloane, N. J. A. Sequences A016114 and A068652 in "The On-Line Encyclopedia of Integer Sequences."