المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Extra Strong Lucas Pseudoprime |
 650
 02:53 صباحاً
date: 24-1-2021 |
Author : Grantham, J. 
Book or Source : "Frobenius Pseudoprimes." https://www.pseudoprime.com/pseudo1.ps 
Page and Part : ...|
Read More
Date: 13-10-2020
901
Date: 5-2-2020
1012
Date: 5-11-2020
1386
|
Given the Lucas sequence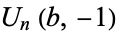 
and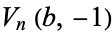 
, define 
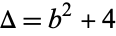. Then an extra strong Lucas pseudoprime to the base 
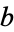is a composite number 
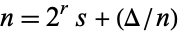, where 
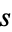is odd and 
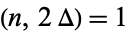such that either 
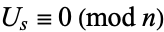and 
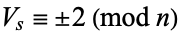, or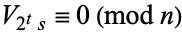 
for some 
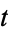with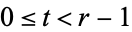 
. An extra strong Lucas pseudoprime is a strong Lucas pseudoprime with parameters 
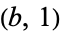. Composite 
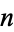are extra strong pseudoprimes for at most 1/8 of possible bases (Grantham 1997).
REFERENCES:
Grantham, J. "Frobenius Pseudoprimes." https://www.pseudoprime.com/pseudo1.ps
Grantham, J. "A Frobenius Probable Prime Test with High Confidence." 1997. https://www.pseudoprime.com/pseudo2.ps
Jones, J. P. and Mo, Z. "A New Primality Test Using Lucas Sequences." Preprint.
Nicely, T. R. "The Baillie-PSW Primality Test." https://www.trnicely.net/misc/bpsw.html.
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
