المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Palindromic Prime |
 1422
 03:49 مساءً
date: 12-1-2021 |
Author : Beiler, A. H. 
Book or Source : Recreations in the Theory of Numbers: The Queen of Mathematical Entertains. New York: Dover, 1964. 
Page and Part : ...|
Read More
Date: 26-10-2020
743
Date: 13-2-2020
1148
Date: 7-8-2020
539
|
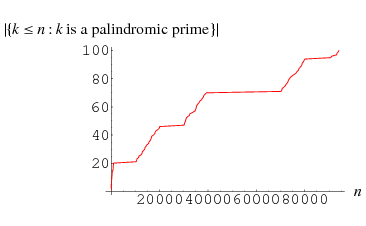
A palindromic prime is a number that is simultaneously palindromic and prime. The first few (base-10) palindromic primes are 2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, ... (OEIS A002385; Beiler 1964, p. 228). The number of palindromic primes less than a given number are illustrated in the plot above. The number of palindromic numbers having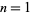 
, 2, 3, ... digits are 4, 1, 15, 0, 93, 0, 668, 0, 5172, 0, ... (OEIS A016115; De Geest) and the total number of palindromic primes less than 10, 
, 
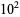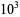, ... are 4, 5, 20, 20, 113, 113, 781, ... (OEIS A050251). Gupta (2009) has computed the numbers of palindromic primes up to 
.
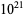The following table lists palindromic primes in various small bases.
 |
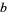OEIS | base-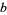 palindromic primes |
| 2 | A117697 | 11, 101, 111, 10001, 11111, 1001001, 1101011, ... |
| 3 | A117698 | 2, 111, 212, 12121, 20102, 22122, ... |
| 4 | A117699 | 2, 3, 11, 101, 131, 323, 10001, 11311, 12121, ... |
| 5 | A117700 | 2, 3, 111, 131, 232, 313, 414, 10301, 12121, 13331, ... |
| 6 | A117701 | 2, 3, 5, 11, 101, 111, 141, 151, 515, ... |
| 7 | A117702 | 2, 3, 5, 131, 212, 313, 515, 535, 616, ... |
| 8 | A006341 | 2, 3, 5, 7, 111, 131, 141, 161, 323, ... |
| 9 | A117703 | 2, 3, 5, 7, 131, 151, 212, 232, 272, 414, ... |
| 10 | A002385 | 2, 3, 5, 7, 11, 101, 131, 151, 181, ... |
Banks et al. (2004) proved that almost all palindromes (in any base) are composite, with the precise statement being
 |
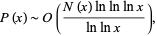(1) |
where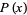 
is the number of palindromic primes 
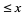and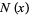 
is the number of palindromic numbers 
.
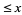The sum of the reciprocals of the palindromic primes converges to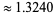 
(OEIS A118064) a number sometimes known as Honaker's constant (Rivera), where the value computed using all palindromic primes 
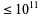is 1.32398... (M. Keith).
The first few palindromic primes formed by taking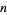 
digits in the decimal expansion of pi and reflecting about the last digit are 3, 313, 31415926535897932384626433833462648323979853562951413, ... (OEIS A039954; Caldwell). These numbers are prime for 
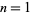, 2, 27, 151, 461, 2056, ... (OEIS A119351), with no others for 
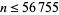(E. W. Weisstein, Mar. 21, 2009).
The first few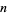 
such that both 
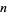and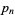 
are palindromic (where 
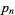is the 
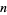th prime) are given by 1, 2, 3, 4, 5, 8114118, ... (OEIS A046942; Rivera), corresponding to 
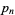of 2, 3, 5, 7, 11, 143787341 (OEIS A046941; Rivera).
Palindromic primes of the form
 |
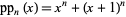(2) |
for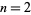 
include 5, 181, 313, 3187813, ... (OEIS A050239; De Geest, Rivera), which occur for 
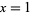, 9, 12, 1262, ... (OEIS A050236; De Geest, Rivera), with no others for 
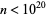and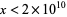 
(De Geest).
As of Nov. 2014, the largest proven palindromic prime is
 |
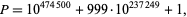(3) |
which has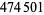 
decimal digits (http://primes.utm.edu/top20/page.php?id=53#records).
REFERENCES:
Banks, W. D.; Hart, D. N.; and Sakata, M. "Almost All Palindromes Are Composite." Math. Res. Lett. 11, 853-868, 2004.
Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematical Entertains. New York: Dover, 1964.
Caldwell, C. "The Top Twenty: Palindrome." http://primes.utm.edu/top20/page.php?id=53#records.
Caldwell, C. "Prime Curios!: 31415...51413 (53-digits)." http://primes.utm.edu/curios/page.php?curio_id=725.
De Geest, P. "Palindromic Numbers and Other Recreational Topics." http://www.worldofnumbers.com/index.shtml.
De Geest, P. "Palindromic Prime Statistics--The Table." http://www.worldofnumbers.com/palprim1.htm.
De Geest, P. "Palindromic Prime Page 3." http://www.worldofnumbers.com/palprim3.htm.
De Geest, P. "Palindromic Sums of Squares of Consecutive Integers." http://www.worldofnumbers.com/sumsquare.htm.
Gupta, S. S. "Palindromic Primes Up to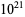 
." 13 Mar 2009. http://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0903&L=nmbrthry&T=0&F=&S=&P=2104.
Jobling, P. "Re: Record Palindrome." 27 Dec 2005. http://groups.yahoo.com/group/primeform/message/6764.
Rivera, C. "Problems & Puzzles: Puzzle 014-Pal-Primes and Sum of Powers." http://www.primepuzzles.net/puzzles/puzz_014.htm.
Rivera, C. "Problems & Puzzles: Puzzle 051-Pi Such that Pi is Palprime & i = Palindrome." http://www.primepuzzles.net/puzzles/puzz_051.htm.
Rivera, C. "Problems & Puzzles: Puzzle 056-The Honaker's Constant." http://www.primepuzzles.net/puzzles/puzz_056.htm.
Sloane, N. J. A. Sequences A002385/M0670, A006341, A016115, A039954, A046941, A046942, A050251, A050236, A050239, A117697, A117698, A117699, A117700, A117701, A117702, A117703, A118064, and A119351 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
