


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-3-2020
Date: 13-11-2019
Date: 27-11-2019
|
If there exists a rational integer  such that, when
such that, when 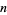 ,
, 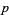 , and
, and 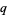 are positive integers,
are positive integers,
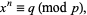 |
then 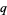 is the
is the 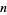 -adic residue of
-adic residue of 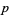 , i.e.,
, i.e., 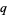 is an
is an 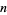 -adic residue of
-adic residue of 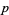 iff
iff 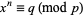 is solvable for
is solvable for  . Reciprocity theorems relate statements of the form "
. Reciprocity theorems relate statements of the form "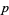 is an
is an 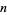 -adic residue of
-adic residue of 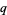 " with reciprocal statements of the form "
" with reciprocal statements of the form "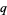 is an
is an 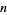 -adic residue of
-adic residue of 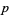 ."
."
The first case to be considered was 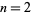 (the quadratic reciprocity theorem), of which Gauss gave the first correct proof. Gauss also solved the case
(the quadratic reciprocity theorem), of which Gauss gave the first correct proof. Gauss also solved the case 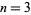 (cubic reciprocity theorem) using integers of the form
(cubic reciprocity theorem) using integers of the form 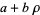 , where
, where 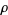 is a root of
is a root of 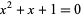 and
and 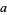 ,
, 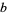 are rational integers. Gauss stated the case
are rational integers. Gauss stated the case 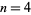 (biquadratic reciprocity theorem) using the Gaussian integers.
(biquadratic reciprocity theorem) using the Gaussian integers.
Proof of 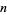 -adic reciprocity for prime
-adic reciprocity for prime 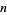 was given by Eisenstein in 1844-50 and by Kummer in 1850-61. In the 1920s, Artin formulated Artin's reciprocity theorem, a general reciprocity law for all orders.
was given by Eisenstein in 1844-50 and by Kummer in 1850-61. In the 1920s, Artin formulated Artin's reciprocity theorem, a general reciprocity law for all orders.
REFERENCES:
Lemmermeyer, F. Reciprocity Laws: Their Evolution from Euler to Artin. Berlin: Springer-Verlag, 2000.
Lemmermeyer, F. "Bibliography on Reciprocity Laws." https://www.rzuser.uni-heidelberg.de/~hb3/recbib.html.
Nagell, T. "Power Residues. Binomial Congruences." §34 in Introduction to Number Theory. New York: Wiley, pp. 115-120, 1951.
Wyman, B. F. "What Is a Reciprocity Law?" Amer. Math. Monthly 79, 571-586, 1972.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|