المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Størmer Number |
 693
 02:29 صباحاً
date: 8-10-2020 |
Author : Sloane, N. J. A 
Book or Source : Sequences A005528/M0950 and A005529/M1505 in "The On-Line Encyclopedia of Integer Sequences." 
Page and Part : ...|
Read More
Date: 24-7-2020
1564
Date: 30-11-2020
616
Date: 30-1-2021
1334
|
A Størmer number is a positive integer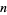 
for which the greatest prime factor 
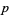of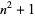 
is at least 
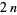. Every Gregory number 
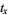can be expressed uniquely as a sum of 
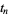s where the 
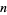s are Størmer numbers. The first few Størmer numbers are given by Conway and Guy (1996) and Todd (1949) and are given by 
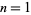, 2, 4, 5, 6, 9, 10, 11, 12, 14, 15, 16, 19, 20, ... (OEIS A005528), corresponding to greatest prime factors 2, 5, 17, 13, 37, 41, 101, 61, 29, ... (OEIS A005529).
REFERENCES:
Conway, J. H. and Guy, R. K. "Størmer's Numbers." The Book of Numbers. New York: Springer-Verlag, pp. 245-248, 1996.
Sloane, N. J. A. Sequences A005528/M0950 and A005529/M1505 in "The On-Line Encyclopedia of Integer Sequences."
Todd, J. "A Problem on Arc Tangent Relations." Amer. Math. Monthly 56, 517-528, 1949.
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
