


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-1-2020
Date: 23-10-2019
Date: 11-1-2021
|
Let  be a real number, and let
be a real number, and let 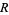 be the set of positive real numbers
be the set of positive real numbers 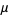 for which
for which
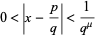 |
(1) |
has (at most) finitely many solutions 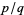 for
for 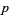 and
and 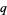 integers. Then the irrationality measure, sometimes called the Liouville-Roth constant or irrationality exponent, is defined as the threshold at which Liouville's approximation theorem kicks in and
integers. Then the irrationality measure, sometimes called the Liouville-Roth constant or irrationality exponent, is defined as the threshold at which Liouville's approximation theorem kicks in and  is no longer approximable by rational numbers,
is no longer approximable by rational numbers,
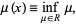 |
(2) |
where 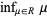 is the infimum. If the set
is the infimum. If the set 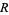 is empty, then
is empty, then 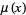 is defined to be
is defined to be 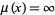 , and
, and  is called a Liouville number. There are three possible regimes for nonempty
is called a Liouville number. There are three possible regimes for nonempty 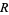 :
:
 |
(3) |
where the transitional case 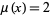 can correspond to
can correspond to  being either algebraic of degree
being either algebraic of degree 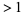 or
or  being transcendental. Showing that
being transcendental. Showing that 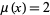 for
for  an algebraic number is a difficult result for which Roth was awarded the Fields medal.
an algebraic number is a difficult result for which Roth was awarded the Fields medal.
The definition of irrationality measure is equivalent to the statement that if  has irrationality measure
has irrationality measure 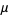 , then
, then 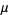 is the smallest number such that the inequality
is the smallest number such that the inequality
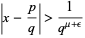 |
(4) |
holds for any 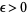 and all integers
and all integers 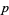 and
and 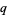 with
with 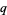 sufficiently large.
sufficiently large.
The irrationality measure of an irrational number  can be given in terms of its simple continued fraction expansion
can be given in terms of its simple continued fraction expansion ![x=[a_0,a_1,a_2,...]](https://mathworld.wolfram.com/images/equations/IrrationalityMeasure/Inline28.gif) and its convergents
and its convergents 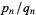 as
as
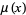 |
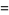 |
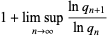 |
(5) |
 |
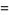 |
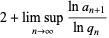 |
(6) |
(Sondow 2004). For example, the golden ratio 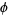 has
has
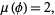 |
(7) |
which follows immediately from (6) and the simple continued fraction expansion ![phi=[1,1,1,...]](https://mathworld.wolfram.com/images/equations/IrrationalityMeasure/Inline37.gif) .
.
Exact values include 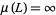 for
for 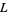 Liouville's constant and
Liouville's constant and 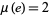 (Borwein and Borwein 1987, pp. 364-365). The best known upper bounds for other common constants as of mid-2020 are summarized in the following table, where
(Borwein and Borwein 1987, pp. 364-365). The best known upper bounds for other common constants as of mid-2020 are summarized in the following table, where 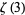 is Apéry's constant,
is Apéry's constant, 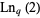 and
and 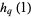 are q-harmonic series, and the lower bounds are 2.
are q-harmonic series, and the lower bounds are 2.
constant  |
upper bound | reference |
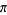 |
7.10320534 | Zeilberger and Zudilin (2020) |
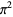 |
5.09541179 | Zudilin (2103) |
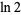 |
3.57455391 | Marcovecchio (2009) |
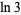 |
5.116201 | Bondareva et al. (2018) |
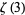 |
5.513891 | Rhin and Viola (2001) |
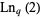 |
2.9384 | Matala-Aho et al. (2006) |
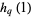 |
2.4650 | Zudilin (2004) |
The bound for 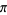 is due to Zeilberger and Zudilin (2020) and improves on the value 7.606308 previously found by Salikhov (2008). It has exact value given as follows. Let
is due to Zeilberger and Zudilin (2020) and improves on the value 7.606308 previously found by Salikhov (2008). It has exact value given as follows. Let 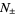 be the complex conjugate roots of
be the complex conjugate roots of
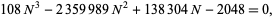 |
(8) |
let 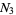 be the positive real root, and let
be the positive real root, and let
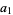 |
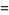 |
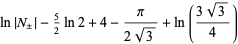 |
(9) |
 |
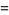 |
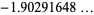 |
(10) |
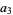 |
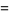 |
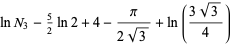 |
(11) |
 |
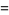 |
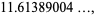 |
(12) |
then the bound is given by
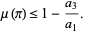 |
(13) |
Alekseyev (2011) has shown that the question of the convergence of the Flint Hills series is related to the irrationality measure of 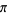 , and in particular, convergence would imply
, and in particular, convergence would imply 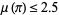 , which is much stronger than the best currently known upper bound.
, which is much stronger than the best currently known upper bound.
REFERENCES:
Alekseyev, M. A. "On Convergence of the Flint Hills Series." http://arxiv.org/abs/1104.5100/. 27 Apr 2011.
Amdeberhan, T. and Zeilberger, D. "q-Apéry Irrationality Proofs by q-WZ Pairs." Adv. Appl. Math. 20, 275-283, 1998.
Beukers, F. "A Rational Approach to Pi." Nieuw Arch. Wisk. 5, 372-379, 2000.
Bondareva, I. V.; Luchin, M. Y.; and Salikhov, V. K. "Symmetrized Polynomials in a Problem of Estimating the Irrationality Measure of the Number 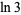 ." Chebyshevskiĭ Sb. 19, 15-25, 2018.
." Chebyshevskiĭ Sb. 19, 15-25, 2018.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, pp. 3-4, 2004.
Borwein, J. M. and Borwein, P. B. "Irrationality Measures." §11.3 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 362-386, 1987.
Finch, S. R. "Liouville-Roth Constants." §2.22 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 171-174, 2003.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford: Clarendon Press, 1979.
Hata, M. "Legendre Type Polynomials and Irrationality Measures." J. reine angew. Math. 407, 99-125, 1990.
Hata, M. "Improvement in the Irrationality Measures of 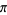 and
and 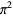 ." Proc. Japan. Acad. Ser. A Math. Sci. 68, 283-286, 1992.
." Proc. Japan. Acad. Ser. A Math. Sci. 68, 283-286, 1992.
Hata, M. "Rational Approximations to 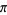 and Some Other Numbers." Acta Arith. 63, 335-349, 1993.
and Some Other Numbers." Acta Arith. 63, 335-349, 1993.
Hata, M. "A Note on Beuker's Integral." J. Austral. Math. Soc. 58, 143-153, 1995.
Hata, M. "A New Irrationality Measure for 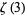 ." Acta Arith. 92, 47-57, 2000.
." Acta Arith. 92, 47-57, 2000.
Marcovecchio, R. "The Rhin-Viola Method for 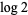 ." Acta Arith. 139, 147-184, 2009.
." Acta Arith. 139, 147-184, 2009.
Matala-Aho, T.; Väänänen, K.; abd Zudilin, W. "New Irrationality Measures for 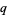 -Logarithms." Math. Comput. 75, 879-889, 2006.
-Logarithms." Math. Comput. 75, 879-889, 2006.
Rhin, G. and Viola, C. "On a Permutation Group Related to 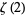 ." Acta Arith. 77, 23-56, 1996.
." Acta Arith. 77, 23-56, 1996.
Rhin, G. and Viola, C. "The Group Structure for 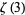 ." Acta Arith. 97, 269-293, 2001.
." Acta Arith. 97, 269-293, 2001.
Rukhadze, E. A. "A Lower Bound for the Rational Approximation of 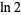 by Rational Numbers." [In Russian]. Vestnik Moskov Univ. Ser. I Math. Mekh., No. 6, 25-29 and 97, 1987.
by Rational Numbers." [In Russian]. Vestnik Moskov Univ. Ser. I Math. Mekh., No. 6, 25-29 and 97, 1987.
Salikhov, V. Kh. "On the Irrationality Measure of 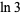 ."Dokl. Akad. Nauk 417, 753-755, 2007. Translation in Dokl. Math. 76, No. 3, 955-957, 2007.
."Dokl. Akad. Nauk 417, 753-755, 2007. Translation in Dokl. Math. 76, No. 3, 955-957, 2007.
Salikhov, V. Kh. "On the Irrationality Measure of 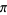 ." Usp. Mat. Nauk 63, 163-164, 2008. English transl. in Russ. Math. Surv 63, 570-572, 2008.
." Usp. Mat. Nauk 63, 163-164, 2008. English transl. in Russ. Math. Surv 63, 570-572, 2008.
Sondow, J. "Irrationality Measures, Irrationality Bases, and a Theorem of Jarnik." Proceedings of Journées Arithmétiques, Graz 2003 in the Journal du Theorie des Nombres Bordeaux. http://arxiv.org/abs/math.NT/0406300.
Stark, H. M. An Introduction to Number Theory. Cambridge, MA: MIT Press, 1994.
van Assche, W. "Little 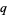 -Legendre Polynomials and Irrationality of Certain Lambert Series." Jan. 23, 2001. http://wis.kuleuven.be/analyse/walter/qLegend.pdf.
-Legendre Polynomials and Irrationality of Certain Lambert Series." Jan. 23, 2001. http://wis.kuleuven.be/analyse/walter/qLegend.pdf.
Zeilberger, D. and Zudilin, W. "The Irrationality Measure of 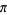 is at Most 7.103205334137...." 8 Jan 2020. https://arxiv.org/abs/1912.06345.
is at Most 7.103205334137...." 8 Jan 2020. https://arxiv.org/abs/1912.06345.
Zudilin, V. V. "An Essay on the Irrationality Measures of 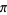 and Other Logarithms." Chebyshevskiĭ Sb. 5, 49-65, 2004.
and Other Logarithms." Chebyshevskiĭ Sb. 5, 49-65, 2004.
Zudilin, V. V. "On the Irrationality Measure of 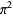 ." Russian Math. Surveys 68, 1133-1135, 2013.
." Russian Math. Surveys 68, 1133-1135, 2013.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|