


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-6-2020
Date: 28-8-2020
Date: 7-1-2021
|
While the Catalan numbers are the number of p-good paths from 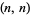 to (0,0) which do not cross the diagonal line, the super Catalan numbers count the number of lattice paths with diagonal steps from
to (0,0) which do not cross the diagonal line, the super Catalan numbers count the number of lattice paths with diagonal steps from 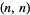 to (0,0) which do not touch the diagonal line
to (0,0) which do not touch the diagonal line 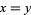 .
.
The super Catalan numbers are given by the recurrence relation
 |
(1) |
(Comtet 1974), with 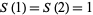 . (Note that the expression in Vardi (1991, p. 198) contains two errors.) A closed form expression in terms of Legendre polynomials
. (Note that the expression in Vardi (1991, p. 198) contains two errors.) A closed form expression in terms of Legendre polynomials 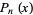 for
for 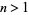 is
is
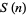 |
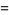 |
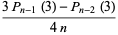 |
(2) |
 |
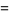 |
![1/4[-P_n(3)+6P_(n-1)(3)-P_(n-2)(3)]](https://mathworld.wolfram.com/images/equations/SuperCatalanNumber/Inline12.gif) |
(3) |
(Vardi 1991, p. 199). The first few super Catalan numbers are 1, 1, 3, 11, 45, 197, ... (OEIS A001003). These are often called the "little" Schröder numbers. Multiplying by 2 gives the usual ("large") Schröder numbers 2, 6, 22, 90, ... (OEIS A006318).
The first few prime super Catalan numbers have indices 3, 4, 6, 10, 216, ... (OEIS A092839), with no others less than 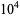 (Weisstein, Mar. 7, 2004), corresponding to the numbers 3, 11, 197, 103049, ... (OEIS A092840).
(Weisstein, Mar. 7, 2004), corresponding to the numbers 3, 11, 197, 103049, ... (OEIS A092840).
REFERENCES:
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, p. 56, 1974.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Exercise 7.50 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Motzkin, T. "Relations Between Hypersurface Cross Ratios and a Combinatorial Formula for Partitions of a Polygon for Permanent Preponderance and for Non-Associative Products." Bull. Amer. Math. Soc. 54, 352-360, 1948.
Schröder, E. "Vier combinatorische Probleme." Z. Math. Phys. 15, 361-376, 1870.
Sloane, N. J. A. Sequences A001003/M2898, A092839, and A092840 in "The On-Line Encyclopedia of Integer Sequences."
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 198-199, 1991.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|