المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Euler,s Totient Theorem |
 889
 06:00 مساءً
date: 27-8-2020 |
Author : Shanks, D 
Book or Source : Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea 
Page and Part : ...|
Read More
Date: 11-1-2021
1434
Date: 25-10-2020
795
Date: 15-12-2020
1070
|
A generalization of Fermat's little theorem. Euler published a proof of the following more general theorem in 1736. Let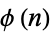 
denote the totient function. Then
 |
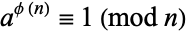for all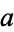 
relatively prime to 
.
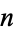REFERENCES:
Séroul, R. "The Theorems of Fermat and Euler." §2.8 in Programming for Mathematicians. Berlin: Springer-Verlag, p. 15, 2000.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 21 and 23-25, 1993.
|
|
|
|
الصين.. طريقة لمنع تطور قصر النظر لدى تلاميذ المدارس
|
|
|
|
|
|
|
ماذا سيحدث خلال كسوف الشمس يوم السبت؟
|
|
|
|
|
|
|
قسم الشؤون الدينية يختتم محاضراته الرمضانية في صحن مرقد أبي الفضل العباس (عليه السلام)
|
|
|
