


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-1-2021
Date: 27-2-2020
Date: 18-7-2020
|
For a real number 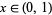 , let
, let 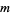 be the number of terms in the convergent to a regular continued fraction that are required to represent
be the number of terms in the convergent to a regular continued fraction that are required to represent 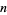 decimal places of
decimal places of  . Then for almost all
. Then for almost all  ,
,
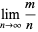 |
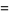 |
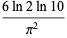 |
(1) |
 |
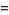 |
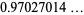 |
(2) |
(OEIS A086819; Lochs 1964). This number is sometimes known as Lochs' constant.
Therefore, the regular continued fraction is only slightly more efficient at representing real numbers than is the decimal expansion. The set of  for which this statement does not hold is of measure 0.
for which this statement does not hold is of measure 0.
REFERENCES:
Bosma, W.; Dajani, K.; and Kraaikamp, C. "Entropy and Counting Correct Digits." Univ. Nijmegen Math. Report 9925, 1999.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
Kintchine, A. "Zur metrischen Kettenbruchtheorie." Compos. Math. 3, 276-285, 1936.
Kraaikamp, C. "A New Class of Continued Fraction Expansions." Acta Arith. 57, 1-39, 1991.
Lévy, P. "Sur le developpement en fraction continue d'un nombre choisi au hasard." Compos. Math. 3, 286-303, 1936.
Lochs, G. "Vergleich der Genauigkeit von Dezimalbruch und Kettenbruch." Abh. Hamburg Univ. Math. Sem. 27, 142-144, 1964.
Perron, O. Die Lehre von den Kettenbrüchen, 3. verb. und erweiterte Aufl. Stuttgart, Germany: Teubner, 1954-57.
Sloane, N. J. A. Sequence A086819 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|