Cototient

The cototient of a positive number 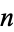 is defined as 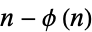, where  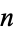is the totient function. It is therefore the number of positive integers  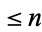that have at least one prime factor in common with .

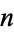The first few cototients for 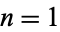, 2, ... are 0, 1, 1, 2, 1, 4, 1, 4, 3, 6, 1, 8, 1, 8, 7, ... (OEIS A051953).

REFERENCES:

Browkin, J. and Schinzel, A. "On Integers Not of the Form 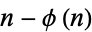." Colloq. Math. 68, 55-58, 1995.

Erdős, P. "Über die Zahlen der Form 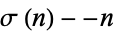 und 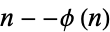." Elem. Math. 11, 83-86, 1973.

Flammenkamp, A. and Luca, F. "Infinite Families of Noncototients." Colloq. Math. 86, 37-41, 2000.

Jamison, R. E. "The Helly Bound for Singular Sums." Disc. Math. 249, 117-133, 2002.

Sloane, N. J. A. Sequence A051953 in "The On-Line Encyclopedia of Integer Sequences."

Pomerance, C. and Yang, H.-S. "Variant of a Theorem of Erdős on the Sum-Of-Proper-Divisors Function." Math. Comput. 83, 1903-1913, 2014.