المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Euclid-Mullin Sequence |
 1448
 02:30 صباحاً
date: 16-1-2021 |
Author : Guy, R. K. and Nowakowski, R. 
Book or Source : "Discovering Primes with Euclid." Delta (Waukesha) 5 
Page and Part : ...|
Read More
Date: 19-2-2020
708
Date: 7-1-2021
872
Date: 10-4-2020
967
|
The sequence of numbers obtained by letting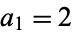 
, and defining
 |
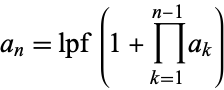where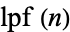 
is the least prime factor. The first few terms are 2, 3, 7, 43, 13, 53, 5, 6221671, 38709183810571, 139, ... (OEIS A000945). Only 43 terms of the sequence are known; the 44th requires factoring a composite 180-digit number.
REFERENCES:
Guy, R. K. and Nowakowski, R. "Discovering Primes with Euclid." Delta (Waukesha) 5, 49-63, 1975.
Mullin, A. A. "Recursive Function Theory." Bull. Amer. Math. Soc. 69, 737, 1963.
Naur, T. "Mullin's Sequence of Primes Is Not Monotonic." Proc. Amer. Math. Soc. 90, 43-44, 1984.
Sloane, N. J. A. Sequence A000945/M0863 in "The On-Line Encyclopedia of Integer Sequences."
Wagstaff, S. S. "Computing Euclid's Primes." Bull. Institute Combin. Applications 8, 23-32, 1993.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
