


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-1-2021
Date: 22-9-2020
Date: 3-11-2020
|
The number of different triangles which have integer side lengths and perimeter 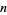 is
is
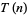 |
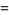 |
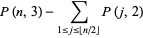 |
(1) |
 |
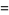 |
![[(n^2)/(12)]-|_n/4_||_(n+2)/4_|](https://mathworld.wolfram.com/images/equations/IntegerTriangle/Inline7.gif) |
(2) |
 |
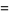 |
![{[(n^2)/(48)] for n even; [((n+3)^2)/(48)] for n odd,](https://mathworld.wolfram.com/images/equations/IntegerTriangle/Inline10.gif) |
(3) |
where 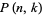 is the partition function giving the number of ways of writing
is the partition function giving the number of ways of writing 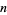 as a sum of exactly
as a sum of exactly 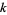 terms,
terms, ![[x]](https://mathworld.wolfram.com/images/equations/IntegerTriangle/Inline14.gif) is the nearest integer function, and
is the nearest integer function, and 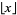 is the floor function (Andrews 1979, Jordan et al. 1979, Honsberger 1985). A slightly complicated closed form is given by
is the floor function (Andrews 1979, Jordan et al. 1979, Honsberger 1985). A slightly complicated closed form is given by
![T(n)=1/(288)[6n^2+18n-9(2n+3)(-1)^n-1
+36sin(1/2pin)-36cos(1/2pin)+64cos(2/3pin)].](https://mathworld.wolfram.com/images/equations/IntegerTriangle/NumberedEquation1.gif) |
(4) |
The values of 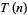 for
for 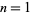 , 2, ... are 0, 0, 1, 0, 1, 1, 2, 1, 3, 2, 4, 3, 5, 4, 7, 5, 8, 7, 10, 8, 12, 10, 14, 12, 16, ... (OEIS A005044), which is also Alcuin's sequence padded with two initial 0s.
, 2, ... are 0, 0, 1, 0, 1, 1, 2, 1, 3, 2, 4, 3, 5, 4, 7, 5, 8, 7, 10, 8, 12, 10, 14, 12, 16, ... (OEIS A005044), which is also Alcuin's sequence padded with two initial 0s.
The generating function for 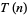 is given by
is given by
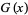 |
 |
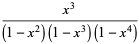 |
(5) |
 |
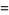 |
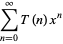 |
(6) |
 |
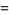 |
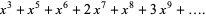 |
(7) |
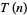 also satisfies
also satisfies
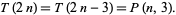 |
(8) |
It is not known if a triangle with integer sides, triangle medians, and area exists (although there are incorrect proofs of the impossibility in the literature). However, R. L. Rathbun, A. Kemnitz, and R. H. Buchholz have shown that there are infinitely many triangles with rational sides (Heronian triangles) with two rational triangle medians (Guy 1994).
REFERENCES:
Andrews, G. "A Note on Partitions and Triangles with Integer Sides." Amer. Math. Monthly 86, 477, 1979.
Buchholz, R. H. "Perfect Pyramids." Bull. Austral. Math. Soc. 45, 353-368, 1992.
Guy, R. K. "Triangles with Integer Sides, Medians, and Area." §D21 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 188-190, 1994.
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 39-47, 1985.
Jordan, J. H.; Walch, R.; and Wisner, R. J. "Triangles with Integer Sides." Amer. Math. Monthly 86, 686-689, 1979.
Pegg, E. Jr. "Triangles" https://www.mathpuzzle.com/triangle.html.
Sloane, N. J. A. Sequence A005044/M0146 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للتخلص من الإمساك.. فاكهة واحدة لها مفعول سحري
|
|
|
|
|
|
|
العلماء ينجحون لأول مرة في إنشاء حبل شوكي بشري وظيفي في المختبر
|
|
|
|
|
|
|
جراح في مستشفى الكفيل: نسعى دائمًا إلى تطوير العمل لإجراء العمليات المتقدمة
|
|
|