


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-11-2020
Date: 7-3-2020
Date: 4-11-2019
|
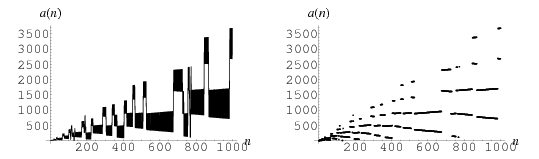
There are at least two sequences attributed to B. Recamán. One is the sequence 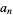 formed by taking
formed by taking 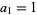 and letting
and letting
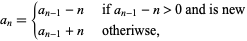 |
(1) |
which can be succinctly defined as "subtract if you can, otherwise add." The first few terms are 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, ... (OEIS A005132), illustrated above.

A view of the first 256 terms as binary bits is shown above.
The terms 1, 2, 3, ... occur at positions 1, 4, 2, 131, 129, 3, 5, ... (OEIS A057167). The high-water marks in this sequence are 1, 4, 131, 99734, 181653, 328002, ... (OEIS A064227), which occur at positions 1, 2, 4, 19, 61, 879, ... (OEIS A064228).
Another sequence defined by Recamán is the sequence obtained by letting 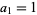 and defining
and defining
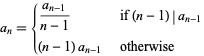 |
(2) |
(Guy and Nowakowski 1995, Sloane 1999). The first few terms of this sequence are 1, 1, 2, 6, 24, 120, 20, 140, 1120, ... (OEIS A008336).
REFERENCES:
Guy, R. K. and Nowakowski, R. J. "Monthly Unsolved Problems, 1696-1995." Amer. Math. Monthly 102, 921-926, 1995.
Sloane, N. J. A. Sequences A005132/M2511, A008336, A057167, A064227, and A064228 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. "My Favorite Integer Sequences." In Sequences and Their Applications (Proceedings of SETA '98) (Ed. C. Ding, T. Helleseth, and H. Niederreiter). London: Springer-Verlag, pp. 103-130, 1999. https://www.research.att.com/~njas/doc/sg.pdf.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|