


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-12-2020
Date: 14-11-2019
Date: 12-9-2020
|
Assume that 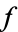 is a nonnegative real function on
is a nonnegative real function on 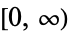 and that the two integrals
and that the two integrals
![int_0^inftyx^(p-1-lambda)[f(x)]^pdx](http://mathworld.wolfram.com/images/equations/Carlson-LevinConstant/NumberedEquation1.gif) |
(1) |
![int_0^inftyx^(q-1+mu)[f(x)]^qdx](http://mathworld.wolfram.com/images/equations/Carlson-LevinConstant/NumberedEquation2.gif) |
(2) |
exist and are finite. If 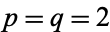 and
and 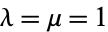 , Carlson (1934) determined
, Carlson (1934) determined
![int_0^inftyf(x)dx<=sqrt(pi)(int_0^infty[f(x)]^2dx)^(1/4)(int_0^inftyx^2[f(x)]^2dx)^(1/4)](http://mathworld.wolfram.com/images/equations/Carlson-LevinConstant/NumberedEquation3.gif) |
(3) |
and showed that 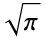 is the best constant (in the sense that counterexamples can be constructed for any stricter inequality which uses a smaller constant). For the general case
is the best constant (in the sense that counterexamples can be constructed for any stricter inequality which uses a smaller constant). For the general case
![int_0^inftyf(x)dx<=C(int_0^inftyx^(p-1-lambda)[f(x)]^pdx)^s(int_0^inftyx^(q-1+mu)[f(x)]^qdx)^t,](http://mathworld.wolfram.com/images/equations/Carlson-LevinConstant/NumberedEquation4.gif) |
(4) |
and Levin (1948) showed that the best constant is
![C=1/((ps)^s(qt)^t)[(Gamma(s/alpha)Gamma(t/alpha))/((lambda+mu)Gamma((s+t)/alpha))]^alpha,](http://mathworld.wolfram.com/images/equations/Carlson-LevinConstant/NumberedEquation5.gif) |
(5) |
where
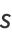 |
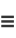 |
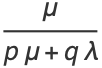 |
(6) |
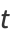 |
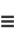 |
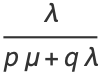 |
(7) |
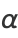 |
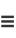 |
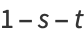 |
(8) |
and 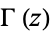 is the gamma function.
is the gamma function.
REFERENCES:
Beckenbach, E. F.; and Bellman, R. "Carlson's Inequality" and "Generalizations of Carlson's Inequality." §5.8 and 5.9 in Inequalities, 2nd rev. printing. New York: Springer-Verlag, pp. 175-177, 1965.
Boas, R. P. Jr. Review of Levin, V. I. "Exact Constants in Inequalities of the Carlson Type." Math. Rev. 9, 415, 1948.
Carlson, F. "Une inégalité." Arkiv för Mat., Astron. och Fys. 25B, 1-5, 1934.
Finch, S. R. "Carlson-Levin Constant." §3.2 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 211-212, 2003.
Levin, V. I. "Exact Constants in Inequalities of the Carlson Type." Doklady Akad. Nauk. SSSR (N. S.) 59, 635-638, 1948. English review in Boas (1948).
Mitrinovic, D. S.; Pecaric, J. E.; and Fink, A. M. Inequalities Involving Functions and Their Integrals and Derivatives. Amsterdam, Netherlands: Kluwer, 1991.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|