
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-9-2020
Date: 27-12-2020
Date: 22-12-2019
|
Consider 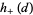 proper equivalence classes of forms with discriminant
proper equivalence classes of forms with discriminant 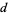 equal to the field discriminant, then they can be subdivided equally into
equal to the field discriminant, then they can be subdivided equally into 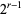 genera of
genera of 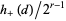 forms which form a subgroup of the proper equivalence class group under composition (Cohn 1980, p. 224), where
forms which form a subgroup of the proper equivalence class group under composition (Cohn 1980, p. 224), where 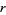 is the number of distinct prime divisors of
is the number of distinct prime divisors of 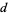 . This theorem was proved by Gauss in 1801.
. This theorem was proved by Gauss in 1801.
REFERENCES:
Arno, S.; Robinson, M. L.; and Wheeler, F. S. "Imaginary Quadratic Fields with Small Odd Class Number." http://www.math.uiuc.edu/Algebraic-Number-Theory/0009/.
Cohn, H. Advanced Number Theory. New York: Dover, 1980.
Gauss, C. F. Disquisitiones Arithmeticae. New Haven, CT: Yale University Press, 1966.



|
|
|
|
الصين.. طريقة لمنع تطور قصر النظر لدى تلاميذ المدارس
|
|
|
|
|
|
|
ماذا سيحدث خلال كسوف الشمس يوم السبت؟
|
|
|
|
|
|
|
قسم الشؤون الدينية يختتم محاضراته الرمضانية في صحن مرقد أبي الفضل العباس (عليه السلام)
|
|
|