المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Baum-Sweet Sequence |
 970
 06:12 مساءً
date: 26-12-2019 |
Author : Allouche, J.-P. and Shallit, J. 
Book or Source : "Example 5.1.7 (The Baum-Sweet Sequence)." Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press 
Page and Part : ...|
Read More
Date: 8-3-2020
614
Date: 11-8-2020
519
Date: 5-12-2020
651
|
The Baum-Sweet sequence is the sequence of numbers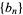 
such that 
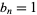if the binary representation of 
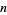contains no block of consecutive 0s of odd length, and 
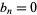otherwise. For 
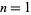, 2, ... the first few terms are 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, ... (OEIS A086747). A recurrence plot of the limiting value of this sequence is illustrated above.
REFERENCES:
Allouche, J.-P. and Shallit, J. "Example 5.1.7 (The Baum-Sweet Sequence)." Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, pp. 156-157, 2003.
Baum, L. E. and Sweet, M. M. "Continued Fractions of Algebraic Power Series in Characteristic 2." Ann. Math. 103, 593-610, 1976.
Sloane, N. J. A. Sequence A086747 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
