


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-10-2020
Date: 17-8-2020
Date: 7-8-2020
|
The negabinary representation of a number 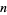 is its representation in base
is its representation in base 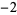 (i.e., base negative 2). It is therefore given by the coefficients
(i.e., base negative 2). It is therefore given by the coefficients 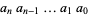 in
in
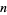 |
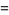 |
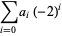 |
(1) |
 |
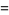 |
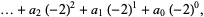 |
(2) |
where 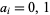 .
.
Conversion of 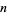 to negabinary can be done using the Wolfram Language code
to negabinary can be done using the Wolfram Language code
Negabinary[n_Integer] := Module[
{t = (2/3)(4^Floor[Log[4, Abs[n] + 1] + 2] - 1)},
IntegerDigits[BitXor[n + t, t], 2]
]
due to D. Librik (Szudzik). The bitwise XOR portion is originally due to Schroeppel (1972), who noted that the sequence of bits in 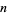 is given by
is given by 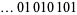 .
.
The following table gives the negabinary representations for the first few integers (OEIS A039724).
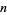 |
negabinary | 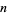 |
negabinary |
| 1 | 1 | 11 | 11111 |
| 2 | 110 | 12 | 11100 |
| 3 | 111 | 13 | 11101 |
| 4 | 100 | 14 | 10010 |
| 5 | 101 | 15 | 10011 |
| 6 | 11010 | 16 | 10000 |
| 7 | 11011 | 17 | 10001 |
| 8 | 11000 | 18 | 10110 |
| 9 | 11001 | 19 | 10111 |
| 10 | 11110 | 20 | 10100 |
If these numbers are interpreted as binary numbers and converted to decimal, their values are 1, 6, 7, 4, 5, 26, 27, 24, 25, 30, 31, 28, 29, 18, 19, 16, ... (OEIS A005351). The numbers having the same representation in binary and negabinary are members of the Moser-de Bruijn sequence, 0, 1, 4, 5, 16, 17, 20, 21, 64, 65, 68, 69, 80, 81, ... (OEIS A000695).
REFERENCES:
Gardner, M. Knotted Doughnuts and Other Mathematical Entertainments. New York: W. H. Freeman, p. 101, 1986.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1998.
Schroeppel, R. Item 128 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 24, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/flows.html#item128.
Sloane, N. J. A. Sequences A000695/M3259, A005351/M4059, and A039724 in "The On-Line Encyclopedia of Integer Sequences."
Szudzik, M. "Programming Challenge: A Mathematica Programming Contest." Wolfram Technology Conference, 1999.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|