Meixner Polynomial of the First Kind

Polynomials 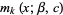 which form the Sheffer sequence for

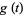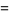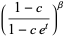			(1)
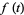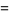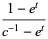			(2)

and have generating function

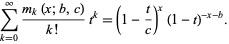(3)

The are given in terms of the hypergeometric series by

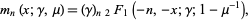(4)

where 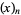 is the Pochhammer symbol (Koepf 1998, p. 115). The first few are

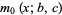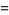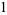			(5)
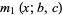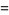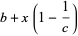			(6)

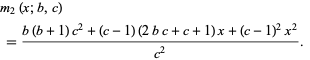(7)

Koekoek and Swarttouw (1998) defined the Meixner polynomials without the Pochhammer symbol as

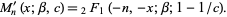(8)

The Krawtchouk polynomials are a special case of the Meixner polynomials of the first kind.

REFERENCES:

Chihara, T. S. An Introduction to Orthogonal Polynomials. New York: Gordon and Breach, p. 175, 1978.

Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 2. New York: Krieger, pp. 224-225, 1981.

Koekoek, R. and Swarttouw, R. F. "Meixner." §1.9 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 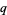-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 45-46, 1998.

Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, p. 115, 1998.

Roman, S. The Umbral Calculus. New York: Academic Press, 1984.

Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., p. 35, 1975.