


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-5-2019
Date: 20-7-2019
Date: 28-4-2019
|
In his last letter to Hardy, Ramanujan defined 17 Jacobi theta function-like functions 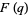 with
with 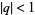 which he called "mock theta functions" (Watson 1936ab, Ramanujan 1988, pp. 127-131; Ramanujan 2000, pp. 354-355). These functions are q-series with exponential singularities such that the arguments terminate for some power
which he called "mock theta functions" (Watson 1936ab, Ramanujan 1988, pp. 127-131; Ramanujan 2000, pp. 354-355). These functions are q-series with exponential singularities such that the arguments terminate for some power 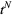 . In particular, if
. In particular, if 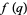 is not a Jacobi theta function, then it is a mock theta function if, for each root of unity
is not a Jacobi theta function, then it is a mock theta function if, for each root of unity 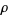 , there is an approximation of the form
, there is an approximation of the form
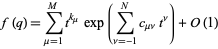 |
(1) |
as 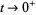 with
with 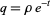 (Gordon and McIntosh 2000).
(Gordon and McIntosh 2000).
If, in addition, for every root of unity 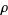 there are modular forms
there are modular forms 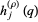 and real numbers
and real numbers 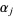 and
and 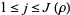 such that
such that
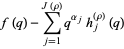 |
(2) |
is bounded as 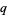 radially approaches
radially approaches 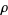 , then
, then 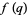 is said to be a strong mock theta function (Gordon and McIntosh 2000).
is said to be a strong mock theta function (Gordon and McIntosh 2000).
Ramanujan found an additional three mock theta functions in his "lost notebook" which were subsequently rediscovered by Watson (1936ab). The first formula on page 15 of Ramanujan's lost notebook relates the functions which Watson calls 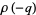 and
and 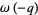 (equivalent to the third equation on page 63 of Watson's 1936 paper), and the last formula on page 31 of the lost notebook relates what Watson calls
(equivalent to the third equation on page 63 of Watson's 1936 paper), and the last formula on page 31 of the lost notebook relates what Watson calls 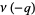 and
and 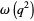 (equivalent to the fourth equation on page 63 of Watson's paper). The orders of these and Ramanujan's original 17 functions were all 3, 5, or 7.
(equivalent to the fourth equation on page 63 of Watson's paper). The orders of these and Ramanujan's original 17 functions were all 3, 5, or 7.
Ramanujan's "lost notebook" also contained several mock theta functions of orders 6 and 10, which, however, were not explicitly identified as mock theta functions by Ramanujan. Their properties have now been investigated in detail (Andrews and Hickerson 1991, Choi 1999).
Unfortunately, while known identities make it clear that mock theta functions of "order" 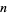 are related to the number
are related to the number 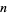 , no formal definition for the order of a mock theta function is known. As a result, the term "order" must be regarded merely as a convenient label when applied to mock theta functions (Andrews and Hickerson 1991).
, no formal definition for the order of a mock theta function is known. As a result, the term "order" must be regarded merely as a convenient label when applied to mock theta functions (Andrews and Hickerson 1991).
The complete list of mock theta functions of order 3 are
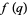 |
 |
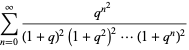 |
(3) |
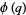 |
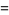 |
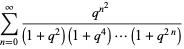 |
(4) |
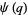 |
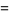 |
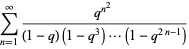 |
(5) |
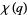 |
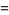 |
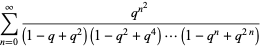 |
(6) |
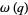 |
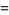 |
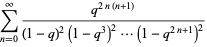 |
(7) |
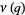 |
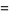 |
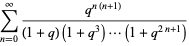 |
(8) |
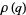 |
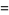 |
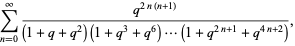 |
(9) |
with 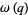 ,
, 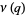 , and
, and 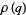 due to Watson (1936ab; Dragonette 1952). Note that the series for
due to Watson (1936ab; Dragonette 1952). Note that the series for 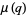 does not converge, but the series of even and odd partial sums do converge, so
does not converge, but the series of even and odd partial sums do converge, so 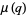 is commonly taken as the average of these two values (Andrews and Hickerson 1991).
is commonly taken as the average of these two values (Andrews and Hickerson 1991).
The following table summarizes the first few terms of these series. 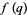 in particular is considered by Dragonette (1952), who showed that the coefficients
in particular is considered by Dragonette (1952), who showed that the coefficients 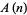 of the series for
of the series for 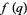 satisfy
satisfy
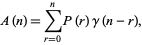 |
(10) |
where 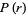 is a partition function P and
is a partition function P and 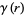 is the sequence 1, 0,
is the sequence 1, 0, 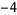 , 4,
, 4, 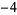 , 4,
, 4, 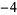 , 8,
, 8, 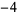 , 8,
, 8, 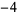 , ... (OEIS A064053) for
, ... (OEIS A064053) for 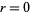 , 1, ....
, 1, ....
| function | OEIS | series |
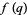 |
A000025 | 1, 1, 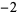 , 3, , 3, 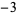 , , 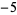 , 7, , 7, 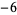 , 6, ... , 6, ... |
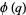 |
A053250 | 1, 1, 0, 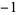 , 1, 1, , 1, 1, 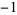 , , 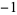 , 0, 2, ... , 0, 2, ... |
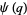 |
A053251 | 0, 1, 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 6, ... |
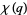 |
A053252 | 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 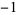 , 0, ... , 0, ... |
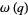 |
A053253 | 1, 2, 3, 4, 6, 8, 10, 14, 18, 22, 29, ... |
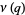 |
A053254 | 1, 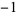 , 2, , 2, 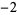 , 2, , 2, 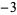 , 4, , 4, 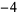 , 5, ... , 5, ... |
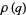 |
A053255 | 1, 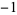 , 0, 1, 0, , 0, 1, 0, 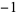 , 1, , 1, 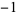 , 0, 1, ... , 0, 1, ... |
Watson (1936ab) proved the fundamental relations connecting Ramanujan's mock theta functions,
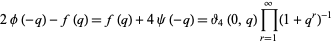 |
(11) |
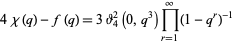 |
(12) |
![2rho(q)+omega(q)=3[1/2q^(-3/8)theta_2(0,q^(3/2))]^2product_(r=1)^(infty)(1-q^(2r))^(-1)](http://mathworld.wolfram.com/images/equations/MockThetaFunction/Inline82.gif) |
(13) |
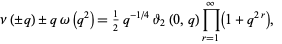 |
(14) |
where 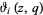 is a Jacobi theta function (Dragonette 1952).
is a Jacobi theta function (Dragonette 1952).
Ramanujan (2000, pp. 354-355) gave 10 mock theta functions of order five, given by
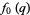 |
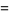 |
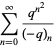 |
(15) |
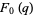 |
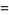 |
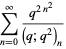 |
(16) |
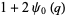 |
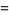 |
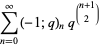 |
(17) |
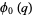 |
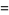 |
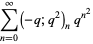 |
(18) |
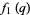 |
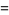 |
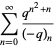 |
(19) |
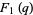 |
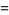 |
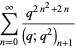 |
(20) |
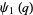 |
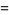 |
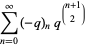 |
(21) |
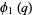 |
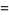 |
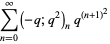 |
(22) |
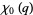 |
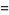 |
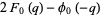 |
(23) |
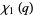 |
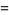 |
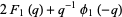 |
(24) |
(Andrews 1986). Note that the notation here follows the standard convention 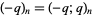 .
.
Ramanujan gave seven mock theta functions of order six, given by
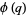 |
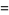 |
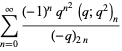 |
(25) |
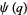 |
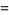 |
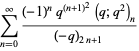 |
(26) |
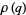 |
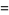 |
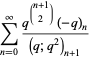 |
(27) |
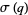 |
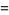 |
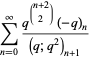 |
(28) |
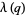 |
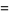 |
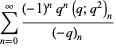 |
(29) |
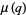 |
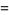 |
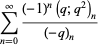 |
(30) |
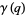 |
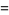 |
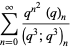 |
(31) |
(Andrews and Hickerson 1991).
Ramanujan (2000, p. 355) also gave three mock theta functions of order seven, given by
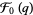 |
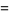 |
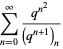 |
(32) |
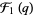 |
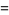 |
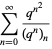 |
(33) |
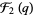 |
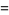 |
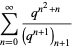 |
(34) |
(Andrews 1986).
Gordon and McIntosh (2000) found eight mock theta functions of order 8,
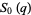 |
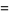 |
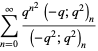 |
(35) |
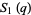 |
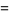 |
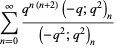 |
(36) |
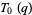 |
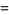 |
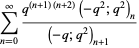 |
(37) |
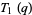 |
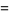 |
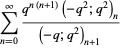 |
(38) |
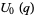 |
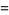 |
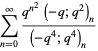 |
(39) |
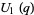 |
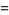 |
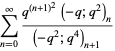 |
(40) |
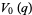 |
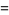 |
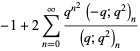 |
(41) |
 |
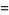 |
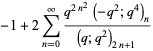 |
(42) |
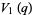 |
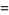 |
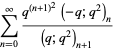 |
(43) |
 |
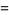 |
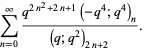 |
(44) |
REFERENCES:
Andrews, G. E. "The Fifth and Seventh Order Mock Theta Functions." Trans. Amer. Soc. 293, 113-134, 1986.
Andrews, G. E. "Mock Theta Functions." Proc. Sympos. Pure Math. 49, 283-298, 1989.
Andrews, G. E. and Berndt, B. Ramanujan's Lost Notebook, Part I. New York: Springer, 2005.
Andrews, G. E. and Hickerson, D. "Ramanujan's 'Lost' Notebook VII: The Sixth Order Mock Theta Functions." Adv. Math. 89, 60-105, 1991.
Bellman, R. E. A Brief Introduction to Theta Functions. New York: Holt, Rinehart, and Winston, p. 51, 1961.
Berndt, B. C. and Rankin, R. A. Ramanujan: Letters and Commentary. Providence, RI: Amer. Math. Soc., pp. 220-224, 1995.
Choi, Y.-S. "Tenth Order Mock Theta Functions in Ramanujan's Lost Notebook." Invent. Math. 136, 497-569, 1999.
Dragonette, L. A. "Some Asymptotic Formulae for the Mock Theta Series of Ramanujan." Trans. Amer. Math. Soc. 73, 474-500, 1952.
Gordon, B. and McIntosh, R. J. "Some Eighth Order Mock Theta Functions." J. London Math. Soc. 62, 321-335, 2000.
Gordon, B. and McIntosh, R. J. "Modular Transformations of Ramanujan's Fifth and Seventh Order Mock Theta Functions." Ramanujan J. 7, 193-222, 2003.
Ramanujan, S. The Lost Notebook and Other Unpublished Manuscripts. New Delhi, India: Narosa, 1988.
Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., 2000.
Selberg, A. "Über die Mock-Thetafunktionen siebenter Ordnung." Arch. Math. og Naturvidenskab 41, 3-15, 1938.
Sloane, N. J. A. Sequences A000025/M0433, A053250, A053251, A053252, A053253, A053254, A053255, and A064053 in "The On-Line Encyclopedia of Integer Sequences."
Watson, G. N. "The Final Problem: An Account of the Mock Theta Functions." J. London Math. Soc. 11, 55-80, 1936a.
Watson, G. N. "The Mock Theta Function (I)." J. London Math. Soc. 11, 55-80, 1936b.
Watson, G. N. "The Mock Theta Function (II)." Proc. London Math. Soc. 42, 274-304, 1937.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|