Maximum

The largest value of a set, function, etc. The maximum value of a set of elements 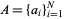 is denoted  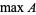or 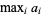, and is equal to the last element of a sorted (i.e., ordered) version of 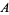. For example, given the set 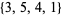, the sorted version is 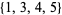, so the maximum is 5. The maximum and minimum are the simplest order statistics.

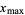The maximum value of a variable  is commonly denoted  (Strang 1988, pp. 286-287 and 301-303) or  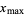(Golub and Van Loan 1996, p. 74). In this work, the convention  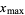is used.

The maximum of a set of elements is implemented in the Wolfram Language as Max[list] and satisfies the identities

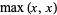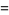			(1)
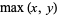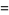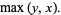			(2)

Definite integrals include

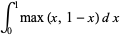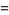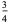			(3)
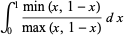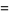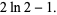			(4)

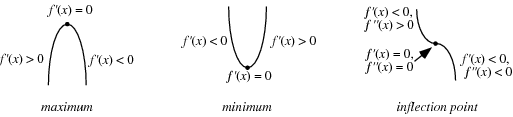
A continuous function may assume a maximum at a single point or may have maxima at a number of points. A global maximum of a function is the largest value in the entire range of the function, and a local maximum is the largest value in some local neighborhood.

For a function 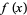 which is continuous at a point 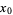, a necessary but not sufficient condition for  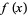to have a local maximum at  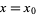is that  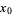be a critical point (i.e.,  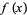is either not differentiable at  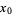or 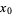 is a stationary point, in which case ).

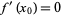The first derivative test can be applied to continuous functions to distinguish maxima from minima. For twice differentiable functions of one variable, 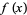, or of two variables, 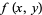, the second derivative test can sometimes also identify the nature of an extremum. For a function 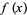, the extremum test succeeds under more general conditions than the second derivative test.

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.

Golub, G. and Van Loan, C. Matrix Computations, 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.

Niven, I. Maxima and Minima without Calculus. Washington, DC: Math. Assoc. Amer., 1982.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Minimization or Maximization of Functions." Ch. 10 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 387-448, 1992.

Strang, G. Linear Algebra and its Applications, 3rd ed. Philadelphia, PA: Saunders, 1988.

Tikhomirov, V. M. Stories About Maxima and Minima. Providence, RI: Amer. Math. Soc., 1991.