Well-Defined

An expression is called "well-defined" (or "unambiguous") if its definition assigns it a unique interpretation or value. Otherwise, the expression is said to not be well-defined or to be ambiguous.

For example, the expression 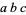 (the product) is well-defined if 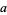, , 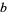and 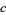 are integers. Because integers are associative,  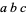has the same value whether it is interpreted to mean  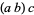or 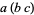. However, if 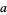, , 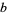and 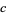 are Cayley numbers, then the expression  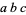is not well-defined, since Cayley numbers are not, in general, associative, so that the two interpretations  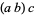and 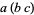 can be different.

Sometimes, ambiguities are implicitly resolved by notational convention. For example, the conventional interpretation of 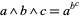 is 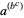, never 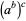, so that the expression  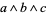is well-defined even though exponentiation is nonassociative.

The term "well-defined" also has a technical meaning in field of partial differential equations. A solution to a partial differential equation that is a continuous function of its values on the boundary is said to be well-defined. Otherwise, a solution is called ill-defined.