Laplace's Equation--Spherical Coordinates

In spherical coordinates, the scale factors are 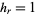, , 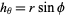, and the separation functions are 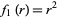, , 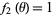, 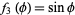giving a Stäckel determinant of .

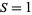The Laplacian is

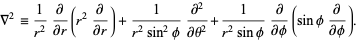(1)

To solve Laplace's equation in spherical coordinates, attempt separation of variables by writing

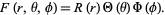(2)

Then the Helmholtz differential equation becomes

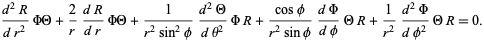(3)

Now divide by ,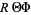

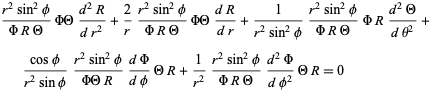(4)

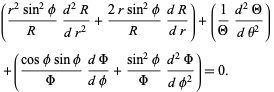(5)

The solution to the second part of (5) must be sinusoidal, so the differential equation is

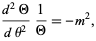(6)

which has solutions which may be defined either as a complex function with , ...,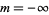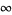 

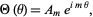(7)

or as a sum of real sine and cosine functions with , ...,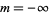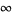 

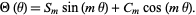(8)

Plugging (6) back into (7),

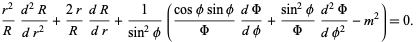(9)

The radial part must be equal to a constant

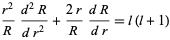(10)

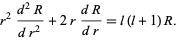(11)

But this is the Euler differential equation, so we try a series solution of the form

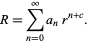(12)

Then

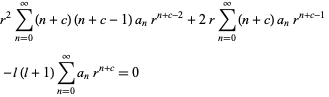(13)

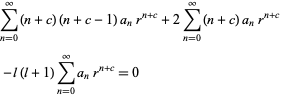(14)

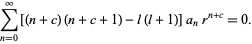(15)

This must hold true for all powers of 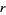. For the  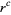term (with ),

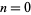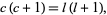(16)

which is true only if 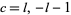 and all other terms vanish. So  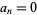for 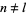, 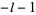. Therefore, the solution of the  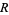component is given by

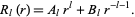(17)

Plugging (17) back into (◇),

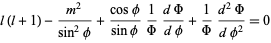(18)

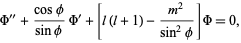(19)

which is the associated Legendre differential equation for 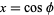 and 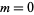, ..., 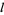. The general complex solution is therefore

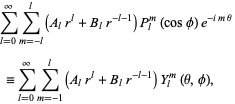(20)

where

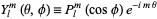(21)

are the (complex) spherical harmonics. The general real solution is

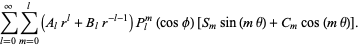(22)

Some of the normalization constants of 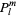 can be absorbed by  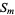and 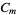, so this equation may appear in the form

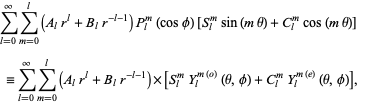(23)

where

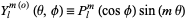(24)

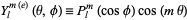(25)

are the even and odd (real) spherical harmonics. If azimuthal symmetry is present, then 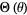 is constant and the solution of the  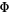component is a Legendre polynomial 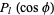. The general solution is then

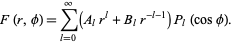(26)

REFERENCES:

Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, p. 244, 1959.

Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, p. 27, 1988.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 514 and 658, 1953.