Heat Conduction Equation--Disk

To solve the heat conduction equation on a two-dimensional disk of radius 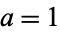, try to separate the equation using

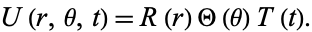(1)

Writing the 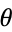 and 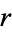 terms of the Laplacian in cylindrical coordinates gives

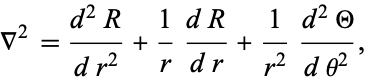(2)

so the heat conduction equation becomes

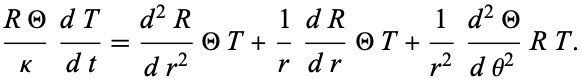(3)

Multiplying through by 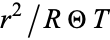 gives

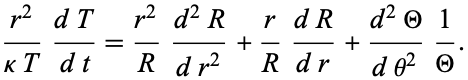(4)

The 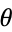 term can be separated.

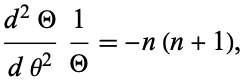(5)

which has a solution

(6)

The remaining portion becomes

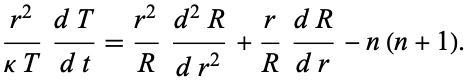(7)

Dividing by 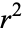 gives

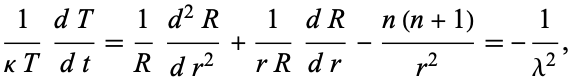(8)

where a negative separation constant has been chosen so that the 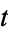 portion remains finite

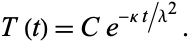(9)

The radial portion then becomes

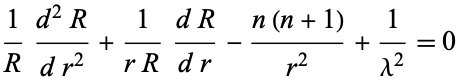(10)

(11)

which is the spherical Bessel differential equation.

Consider disk or radius 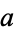 with initial temperature  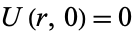and the boundary condition 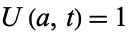. Then the solution is

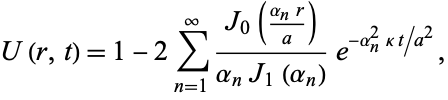(12)

where 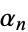 is the 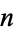th positive zero of the Bessel function of the first kind  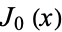(Bowman 1958, pp. 37-39).

REFERENCES:

Bowman, F. Introduction to Bessel Functions. New York: Dover, 1958.

Carslaw, H. S. and Jaeger, J. C. "Some Two-Dimensional Problems in Conduction of Heat with Circular Symmetry." Proc. London Math. Soc. 46, 361-388, 1940.