فضاء الضرب الداخلي-الضرب الداخلي
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
303-308
17-3-2016
43088
سبق وأن تطرقنا في المواضيع السابقة مفاهيم كثيرة كطول المتجه والزاوية المحصورة بين المتجهات في Rn باستخدام ضرب المتجهات النقطي. في هذا الفصل سندرس هذه المفاهيم في فضاء المتجهات وبشكل أكثر عمومية.
تعريف (1-1):
الضرب الداخلي على V هو دالة ترفق العدد الحقيقي <u,v> مع زوج من المتجهات v, u في V بطريقة بحيث تتحقق الشروط الآتية:
ملاحظة:
(1) فضاء المتجهات الحقيقي مع الضرب الداخلي يسمى فضاء الضرب الداخلي الحقيقي.
(2) إذا كانت v = (v1, v2, …. , vn) و u = u1, u2, … , un) متجهات في Rn فإن الصيغة:
تعرف الضرب الداخلي على Rn.
تعريف (1-2) :
لتكن V فضاء الضرب الداخلي فإن طول المتجه u في V يعرف بالشكل:
أما المسافة بين المتجهين u,v ، تكتب d(v , u) ، فتعرف
وقابلة للانعكاس. فإذا كان u . v هو ضرب داخلي إقليدي على Rn فإن الصيغة:
تعرف الضرب الداخلي المسمى الضرب الداخلي على R" المتولد بواسطة A. يمكن كتابة الصيغة أعلاه بالشكل:
مثال(1):
من المعروف في الهندسة الاقليدية أن مجموع طولي ضلعين في مثلث أصغر أو تساوي طول الضلع الثالث كما وأن مجموع مربعات أقطار متوازي الأضلاع يساوي مجموع مربعات الجوانب الأربعة (لاحظ الشكل (1-1) ).
شكل (1-1)
أما كرة الوحدة في هذا الفضاء فتعرف بأنها مجموعة جميع المصفوفات سعة 2 x 2 والتي عناصرها تحقق المعادلة ||V|| = 1، أي
مثال(2)
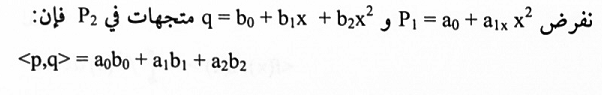
تمثل تعريف الضرب الداخلي على P2
أما طول متعددة الحدود نسبة لهذا الضرب الداخلي فيعرف
كرة الوحدة في هذا الفضاء تتكون من جميع متعددات الحدود p و p2 التي تحقق ||P|| = 1 او 
مثال(3):
لتكن f(x) g(x) , دوال مستمرة على الفترة [a, b] فإن <f,g> المعرفة:
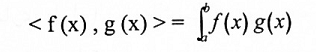
يمثل ضرب داخلي على [a, b].
لكي نبرهن أن <f(x),g(x)> ضرب داخلي يجب أن تحقق شروط التعريف (1-1):
لاحظ ان طول المنحني y = f(x) على الفترة [a, b] يختلف عن طول المتجه f(x) على [a, b] حيث أن طول المنحني هو
لذا فإن الصيغة (4) تختلف عن الصيغة (5).
مبرهنة (1-3):
(خواص فضاء الضرب الداخلي الحقيقي).
لتكن w, u, v ثلاث متجهات في فضاء الضرب الداخلي الحقيقي و k كمية ثابتة، فإن
البرهان:
نبرهن الحالة الثانية.
مثال(4):
الاكثر قراءة في الجبر الخطي
اخر الاخبار
اخبار العتبة العباسية المقدسة
