المتجهات في فضاء البعد الثاني وفضاء البعد الثالث-الضرب الاتجاهي (الضرب التقاطعي)
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
163-175
7-3-2016
57610
الضرب الاتجاهي (الضرب التقاطعي):
كثيراً من تطبيقات المتجهات في الفيزياء والهندسة تحتاج إلى معرفة المتجه المرسوم في الفضاء 3- الذي يكون عمودياً على متجهين معلومين. سنحاول في هذا البند التعريف بأحد انواع المتجهات الذي يعطينا ذلك المتجه.
تعريف (1-1): لكت v = (v1 , v2 , v3) و u = (u1 , u2, u3) متجهان مرسومان في فضاء 3- فإن الضرب الاتجاهي ،يكتب v x u، يعرف:
إن حفظ الصيغة اعلاه قد يبدو صعباً، لذا نقترح الطريقة الآتية لإيجاد مركبات v x u.
1. نرتب مركبات v و u بشكل مصفوفة سعتها 2 x 3.
2. نوجد المركبة الاولى للمتجه v x u بحذف العمود الأول ونأخذ محدد المصفوفة الباقية فنحصل على:
3. نوجد المركبة الثانية للمتجه v x u بحذف العمود الثاني ونأخذ سالب محدد المصفوفة الباقية:
4. نحذف العمود الثالث من المصفوفة الأصلية وبأخذ محدد المصفوفة المتبقية نحصل على:
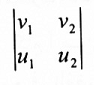
مثال (1):
أوجد v x u إذا علمت ان v = (4-, 0,2) و u = (1,3,-3)
الحل:
نجد مصفوفة مركبات v و u:
ملاحظة:
الضرب النقطي v.u هو كمية ثابتة بينما الضرب الاتجاهي v x u فهو متجه. كما وأن المتجه v x u عمودي على كل من v و u.
مبرهنة (1-2):
إذا كانت w,u,v متجهات مرسومة في فضاء 3- فإن:
1. v. (v x u) = 0 (v x u عمود على v).
2. u. (v x u) ( v x u عمود على v).
البرهان:
نبرهن الحالة (1)
مثال(2):
لتكن v = (2,3,-4) ، u = (1,-1,2) . احسب u x v ثم برهن أن u x v عمودياً على كل من u و v.
الحل:
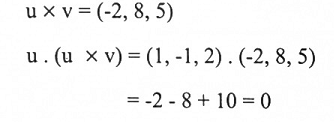
وبنفس الطريقة v. (u x v) = 0
لذا فإن u x v متجهات في فضاء 3- و k كمية ثابتة فإن:
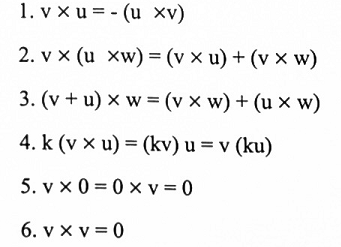
البرهان:
نكتب المصفوفة:
لتكن i = (1,0,0)، j = (0,1,0) ، k = (0,0,1) هذه المتجهات تسمى متجهات الوحدة القياسية في فضاء 3- وتقع على امتداد الإحداثيات الثلاثية (الشكل (3-23). وأن أي متجه مثل v = (v1,v2,v3)يمكن التعبير عنه بدلالة k,j,i وكالآتي:
شكل1-1
شكل (1-2)
ولسهولة حفظ هذه العلاقات يمكن تمثيل ذلك باستخدام الشكل (1-2)، حيث أن الضرب الاتجاهي لأي متجهين قياسيين باتجاه عقارب الساعة يساوي المتجه الثالث بإشارة موجبة والضرب عكس عقارب الساعة فيساوي المتجه الثالث بإشارة سالبة.
ملاحظة:
يمكن التعبير عن الضرب الاتجاهي باستخدام k , j , i وكما يأتي:
مثال (3):
لتكن v = (1,0,-2) و u = (3,2,1) فإن:
مبرهنة (1-4):
إذا كانت v و u متجهان في فضاء 3-، فإن || v x u|| تساوي مساحة متوازي الأضلاع المتكونة بواسطة v و u.
البرهان:
من المبرهنة (1-2) (3) لدينا:
لكن ||u||sin⍉ هو ارتفاع متوازي الأضلاع المتكون من v و u. لذا فإن مساحته A (شكل 1-3) هي:
شكل (1-3)
مثال(4):
أوجد مساحة متوازي الأضلاع الذي رؤوسه P = (1,3,-2) ، Q (2,1,4) و R(-3,1,60)
الحل:
شكل (1-4)
تعريف (1-5):
إذا كانت w, u, v متجهات في فضاء 3-، فإن v. (u x w) يقال له الضرب الثلاثي النقطي.
من الممكن إيجاد الضرب الثلاثي النقطي للمتجهات v = (v1, v2, v3) و u = (u1 , u2, u3) و w = (w1 , w2 , w3) من الصيغة:
مثال (5):
أوجد الضرب الثلاثي النقطي للمتجهات:
تمرين (1): مساحة متوازي الأضلاع في فضاء 2- المتكون من u = (u1 , u2) و u = (u1 , u2) تساوي القيمة المطلقة للمحدد:
(2) حجم متوازي المستطيلات ف فضاء 3 المتكون بوساطة المتجهات
يساوي القيمة المطلقة للمحدد:
الحل:
(1) من الممكن استعمال مبرهنة (1-4) لبرهان الحالة (1) من خلال اعتبار v = (v1 , v2) و u = (u1, u2) متجهات مرسومة ف الفضاء الجزئي xy من النظام الثلاثي الأبعاد xyz (شكل 1-5). في هذه الحالة v = (v1, v2, 0) و (u1, u2, 0). لذا
وبموجب المبرهنة (1-4) وحقيقة كون ||K|| = 1، المساحة A لمتوازي الأضلاع المحدد بالمتجهات U , V:
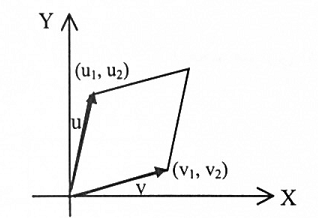
شكل (1-5)
(2) قاعدة متوازي المستطيلات المتكونة من المتجهات W , U, V عبارة عن متوازي الأضلاع المتكونة بواسطة w , u (شكل 1-6).
عليه وبموجب مبرهنة (1-4) فإن مساحة القاعدة هي ||u x w||، وارتفاع متوازي المستطيلات h هو طول المسقط العمودي للمتجه v على u x w.
لذا بموجب الصيغة (9) في (الضرب النقطي , المساقط)
شكل (1-6)
عليه فحجم متوازي المستطيلات:
V = القاعدة × الارتفاع
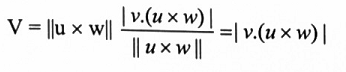
وبموجب الصيغة (5)
مثال(6): أوجد حجم متوازي المستطيلات المحدد بالمتجهات v = (4,1,1) و u = (2,1,0) و w = (0,2,3) الحل:
تعريف (1-6):
المستويين 1 πو π2 متوازيين إذا كان حاصل ضربهما الاتجاهي يساوي صفراً (π1 x π2 = 0)
مثال (7):
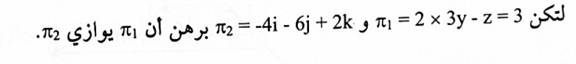
الحل:
وكذلك n1xn2=0 فإن المستويان متوازيين لاحظ الشكل (1-7)
الاكثر قراءة في الجبر الخطي
اخر الاخبار
اخبار العتبة العباسية المقدسة
