فضاء المتجهات الحقيقي:

درسنا في السابق فضاء المتجهات الإقليدي . سنحاول في هذا الفصل تسليط الضوء على فضاءات أخرى إضافة للفضاء الإقليدي مثل المصفوفات ومتعددات الحدود وغيرها.

تعريف (1-1):

تسمى المجموعة غير الخالية V مع عمليتين ثنائيتين معرفتين هما الجمع والضرب بعدد ثابت، فضاء متجهات على الأعداد الحقيقية، إذا تحقق الشروط الآتية:

ملاحظة:

1- عملية الجمع يرمز لها + والضرب بعدد ثابت يعني ضرب v بالعدد k (أي kv).

2. تسمى عناصر V متجهات.

3. الرمز A₁ استخدم هنا لشروط الجمع، أما m₁ فقد استخدمت للضرب (لسهولة حفظها).

مثال(1):

المجموعة V=R^nمع عمليتي الجمع والضرب بعدد ثابت والمعرفة في (1.1) تحقق الشروط أعلاه. عليه فهي قضاء متجهات.

مثال(2): لتكن {0}V = ، أي أن V تحوي على عنصر واحد هو 0، فإن V تحقق شروط        ( 1-1) جميعها فهي إذن فضاء متجهات.

مثال(3):

لتكن V={(a,b):b=ka} حيث k عدد حقيقي ثابتة و a عدد حقيقي. عليه فإن V تحتوي على جميع النقاط الواقعة على الخط المستقيم b = ka المار بنقطة الأصل والذي ميله k ولما كان

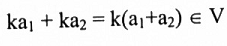
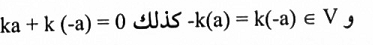
فإن الشرطان A₁ و A₅ متحققان. بما أن بقية الشروط يمكن إثباتها بسهولة. لذا فإن V فضاء متجهات.

مثال(4):

نفرض {y:y = 2x + 1 } V =  حيث x عدد حقيقي. لاحظ أن V مجموعة جميع النقاط الواقعة على الخط المستقيم V .y = wx+1 لا تكون فضاء متجهات لأن شرط الأنغلاق الجمعي لا يتحقق وذلك لأن:

مثال(5):

لتكنV=P n(x)مجموعة جميع متعددات الحدود من الدرجة أصفر أو تساوي n. أي:

حيث a_i أعداد حقيقية. فإن V فضاء متجهات لأن:

 الشرط A_s متحقق. بالاستمرار على نفس الطريقة يمكننا برهان الشروط الاخرى. إذن V=P n(x). فضاء متجهات.

مثال(6):

إذا كانت . فإن مجموعة جميع النقاط في R² التي تكون الربعين الأول والثاني K ليست فضاء متجهات لأن على سبيل المثال ، النقطة (1,1) ليست لها معكوس في V V] ∌ -1,-1)].

مبرهنة (1-2):

لتكن V فضاء متجهات، v∊V و K كمية ثابتة، فإن :

1. 0V = 0

2. K0 = 0

3. (-1) v = -v

4. إذا kv = 0 فإن K = 0 او v = 0

البرهان:

نبرهن (2) و (3).

2. بما أن 0 + 0 = 0 [A₄ مبرهنة (1-1) ].

إذن  k (0+0) = K0 + ko = K0 [m₃ مبرهنة (1-1) ].

بإضافة –k0 للطرفين:

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-الفضاء الاقليدي النوني

فضاء المتجهات العام-رتبة المصفوفات بعد الفضاء الصفري

فضاء المتجهات العام-فضاء الصفوف وفضاء الأعمدة والفضاء الصفري

فضاء المتجهات العام- الأساس والبعد

فضاء المتجهات العام-الفضاءات الجزئية

فضاء الضرب الداخلي-الأساسات المتعامدة طريقة كرام ــ شمت

فضاء الضرب الداخلي-الضرب الداخلي

فضاء الضرب الداخلي-المصفوفات المتعامدة، تبديل الأساسات

فضاء الضرب الداخلي-الزوايا والتعامد في فضاء الضرب الداخلي

أنظمة المعادلات الخطية والمصفوفات -تمارين محلولة