As a result of the dependence of the mass on velocity and Newton’s laws, the changes in the kinetic energy of an object resulting from the total work done by the forces on it always comes out to be

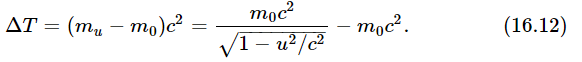
We even went further, and guessed that the total energy is the total mass times c². Now we continue this discussion.

Suppose that our two equally massive objects that collide can still be “seen” inside M. For instance, a proton and a neutron are “stuck together,” but are still moving about inside of M. Then, although we might at first expect the mass M to be 2m₀, we have found that it is not 2m₀, but 2m_w. Since 2m_w is what is put in, but 2m₀ are the rest masses of the things inside, the excess mass of the composite object is equal to the kinetic energy brought in. This means, of course, that energy has inertia. In the last chapter we discussed the heating of a gas, and showed that because the gas molecules are moving and moving things are heavier, when we put energy into the gas its molecules move faster and so the gas gets heavier. But in fact, the argument is completely general, and our discussion of the inelastic collision shows that the mass is there whether or not it is kinetic energy. In other words, if two particles come together and produce potential or any other form of energy; if the pieces are slowed down by climbing hills, doing work against internal forces, or whatever; then it is still true that the mass is the total energy that has been put in. So, we see that the conservation of mass which we have deduced above is equivalent to the conservation of energy, and therefore there is no place in the theory of relativity for strictly inelastic collisions, as there was in Newtonian mechanics. According to Newtonian mechanics it is all right for two things to collide and so form an object of mass 2m₀ which is in no way distinct from the one that would result from putting them together slowly. Of course, we know from the law of conservation of energy that there is more kinetic energy inside, but that does not affect the mass, according to Newton’s laws. But now we see that this is impossible; because of the kinetic energy involved in the collision, the resulting object will be heavier; therefore, it will be a different object. When we put the objects together gently, they make something whose mass is 2m₀; when we put them together forcefully, they make something whose mass is greater. When the mass is different, we can tell that it is different. So, necessarily, the conservation of energy must go along with the conservation of momentum in the theory of relativity.

This has interesting consequences. For example, suppose that we have an object whose mass M is measured, and suppose something happens so that it flies into two equal pieces moving with speed w, so that they each have a mass m_w. Now suppose that these pieces encounter enough material to slow them up until they stop; then they will have mass m₀. How much energy will they have given to the material when they have stopped? Each will give an amount (m_w−m₀) c², by the theorem that we proved before. This much energy is left in the material in some form, as heat, potential energy, or whatever. Now 2m_w=M, so the liberated energy is E=(M−2m₀)c². This equation was used to estimate how much energy would be liberated under fission in the atomic bomb, for example. (Although the fragments are not exactly equal, they are nearly equal.) The mass of the uranium atom was known—it had been measured ahead of time—and the atoms into which it split, iodine, xenon, and so on, all were of known mass. By masses, we do not mean the masses while the atoms are moving, we mean the masses when the atoms are at rest. In other words, both M and m₀ are known. So, by subtracting the two numbers one can calculate how much energy will be released if M can be made to split in “half.” For this reason, poor old Einstein was called the “father” of the atomic bomb in all the newspapers. Of course, all that meant was that he could tell us ahead of time how much energy would be released if we told him what process would occur. The energy that should be liberated when an atom of uranium undergoes fission was estimated about six months before the first direct test, and as soon as the energy was in fact liberated, someone measured it directly (and if Einstein’s formula had not worked, they would have measured it anyway), and the moment they measured it they no longer needed the formula. Of course, we should not belittle Einstein, but rather should criticize the newspapers and many popular descriptions of what causes what in the history of physics and technology. The problem of how to get the thing to occur in an effective and rapid manner is a completely different matter.

The result is just as significant in chemistry. For instance, if we were to weigh the carbon dioxide molecule and compare its mass with that of the carbon and the oxygen, we could find out how much energy would be liberated when carbon and oxygen form carbon dioxide. The only trouble here is that the differences in masses are so small that it is technically very difficult to do.

Now let us turn to the question of whether we should add m₀c² to the kinetic energy and say from now on that the total energy of an object is mc². First, if we can still see the component pieces of rest mass m₀ inside M, then we could say that some of the mass M of the compound object is the mechanical rest mass of the parts, part of it is kinetic energy of the parts, and part of it is potential energy of the parts. But we have discovered, in nature, particles of various kinds which undergo reactions just like the one we have treated above, in which with all the study in the world, we cannot see the parts inside. For instance, when a K-meson disintegrates into two pions it does so according to the law (16.11), but the idea that a K is made out of 2 π’s is a useless idea, because it also disintegrates into 3 π’s!

Therefore we have a new idea: we do not have to know what things are made of inside; we cannot and need not identify, inside a particle, which of the energy is rest energy of the parts into which it is going to disintegrate. It is not convenient and often not possible to separate the total mc² energy of an object into rest energy of the inside pieces, kinetic energy of the pieces, and potential energy of the pieces; instead, we simply speak of the total energy of the particle. We “shift the origin” of energy by adding a constant m₀c² to everything, and say that the total energy of a particle is the mass in motion times c², and when the object is standing still, the energy is the mass at rest times c².

Finally, we find that the velocity v, momentum P, and total energy E are related in a rather simple way. That the mass in motion at speed v is the mass m₀ at rest divided by 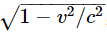, surprisingly enough, is rarely used. Instead, the following relations are easily proved, and turn out to be very useful:

مواضيع ذات صلة

Relativistic mass

Transformation of velocities

The twin paradox

Equivalence of mass and energy

Relativistic dynamics

The Lorentz contraction

Transformation of time

The Michelson-Morley experiment

نظرية المفعول الكهروضوئي ونقد معادلة ط = ك × سر2 للعالم حسن كامل الصباح:

معادلة أينشتاين جامدة المضمون

تاريخ المعادلة المشهورة الطاقة = الكتلة × مربع سرعة الضوء ط = ك × سر2

النسبية الخاصة.. نظرية بوانكاريه